Решите систему уравнений. Оформление кривое, ничего поделать не могу, желательно с объяснением.

👇

Увидеть ответ

Ответ:

gaga2244

06.12.2021

Объяснение:

Решение на фото

4,4(27 оценок)

Ответ:

даньго

06.12.2021

решение смотрите во вложении

4,4(83 оценок)

Открыть все ответы

Ответ:

katirina61171Rfn

06.12.2021

Это дифференциальное уравнение второго порядка с правой частью и относиться ко второму типу.
Нужно найти общее решение неоднородного уравнения в следующем виде

yо.н. = yo.o. + yч.н.

где уо.о. - общее решение однородного уравнения, уч.н. - частное решение.

1. Найдем общее решение дифференциального уравнения соответствующего однородного уравнения :

y''+9y=0

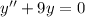
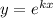Осуществив замену Эйлера $y=e^{kx}$ получим характеристическое уравнение: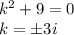
$k^2+9=0\\ k=\pm3i$

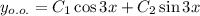
Общее решение однородного уравнения: $y_{o.o.}=C_1\cos 3x+C_2\sin 3x$

2. Нахождение частного решения неоднородного ДУ.
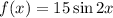Рассмотрим $f(x)=15\sin 2x$ ;
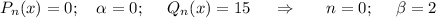
$P_n(x)=0;~~~ \alpha =0;~~~~ Q_n(x)=15~~~~\Rightarrow~~~~~ n=0;~~~~ \beta =2$

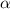Сравнивая $\alpha$ с корнями характеристического уравнения и, принимая во внимая, что n=0

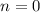, частное решение будем искать в виде: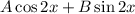
у ч.н. = $A\cos 2x+B\sin2x$

Найдем вторую производную частного решения:
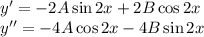
$y'=-2A\sin2x+2B\cos2x\\ y''=-4A\cos2x-4B\sin2x$

Подставив эти данные в исходное уравнение, получим
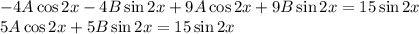
$-4A\cos2x-4B\sin2x+9A\cos 2x+9B\sin2x=15\sin2x\\ 5A\cos2x+5B\sin2x=15\sin2x$

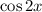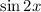
Приравниваем коэффициенты при $\cos2x$ и $\sin2x$
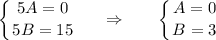
$\displaystyle \left \{ {{5A=0} \atop {5B=15}} \right. ~~~~\Rightarrow~~~~~ \left \{ {{A=0} \atop {B=3}} \right.$

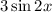
Частное решение: уч.н. = $3\sin2x$

Тогда общее решение неоднородного уравнения:
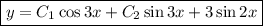
$\boxed{y=C_1\cos3x+C_2\sin3x+3\sin2x}$

4,6(51 оценок)

Ответ:

Alina23154784

06.12.2021

1) A(5,6,4) , B(6,9,4) , C(2,10,10) .
Уравнение плоскости, проходящей через три точки:

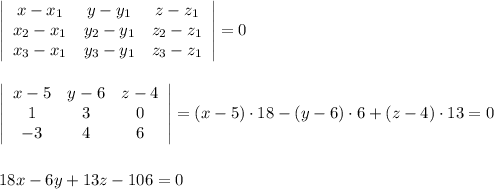
$\left|\begin{array}{ccc}x-x_1&y-y_1&z-z_1\\x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&y_3-y_1&z_3-z_1\end{array}\right| =0\\\\\\\left|\begin{array}{ccc}x-5&y-6&z-4\\1&3&0\\-3&4&6\end{array}\right| =(x-5)\cdot 18-(y-6)\cdot 6+(z-4)\cdot 13=0\\\\\\18x-6y+13z-106=0$

Расстояние от точки М(1,2,3) до плоскости найдём по формуле:

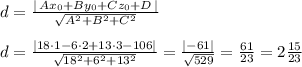
$d=\frac{|\, Ax_0+By_0+Cz_0+D\, |}{\sqrt{A^2+B^2+C^2}}\\\\d=\frac{|18\cdot 1-6\cdot 2+13\cdot 3-106|}{\sqrt{18^2+6^2+13^2}}=\frac{|-61|}{ \sqrt{529} }=\frac{61}{23} =2 \frac{15}{23}$

2) Векторы образуют базис, если они ЛНЗ, то есть определитель, составленный из координат этих векторов отличен от 0 .

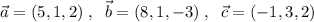
$\vec{a}=(5,1,2)\; ,\; \; \vec{b}=(8,1,-3)\; ,\; \; \vec{c}=(-1,3,2)$

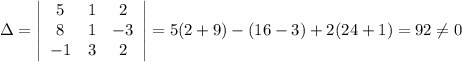
$\Delta = \left|\begin{array}{ccc}5&1&2\\8&1&-3\\-1&3&2\end{array}\right| =5(2+9)-(16-3)+2(24+1)=92\ne 0$

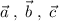Векторы $\vec{a}\; ,\; \vec{b}\; ,\; \vec{c}$ образуют базис. Значит, вектор 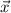$\vec{x}$ можно разложить по данному базису.
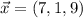Найдём координаты вектора $\vec{x}=(7,1,9)$ в этом базисе, используя соотношение между векторами
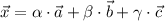$\vec{x}= \alpha \cdot \vec{a}+ \beta \cdot \vec{b}+\gamma \cdot \vec{c}$ .
В координатной форме это соотношение будет иметь вид:

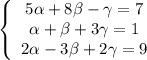
$\left\{\begin{array}{c}5 \alpha +8 \beta -\gamma=7\\ \alpha + \beta +3\gamma =1\\2 \alpha -3 \beta +2\gamma=9\end{array}\right$

Решим систему методом Гаусса.

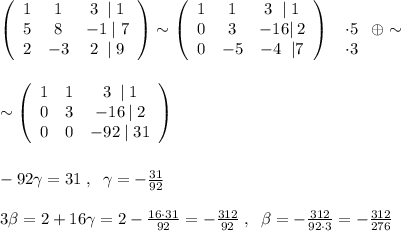
$\left(\begin{array}{ccc}1&1&3\; \; |\; 1\\5&8&-1\; |\; 7\\2&-3&2\; \; |\; 9\end{array}\right) \sim \left(\begin{array}{ccc}1&1&3\; \; |\; 1\\0&3&-16|\, 2\\0&-5&-4\; \; |7\end{array}\right) \; \left\begin{array}{ccc}\\\cdot5\\\cdot 3\end{array}\right \oplus\sim \\\\\\ \sim \left(\begin{array}{ccc}1&1&3\; \; |\; 1\\0&3&-16\, |\; 2\\0&0&-92\; |\; 31\end{array}\right) \\\\\\-92\gamma=31\; ,\; \; \gamma=- \frac{31}{92} \\\\3 \beta =2+16\gamma =2- \frac{16\cdot31}{92}=-\frac{312}{92}\; ,\; \; \beta =-\frac{312}{92\cdot 3}=-\frac{312}{276}$

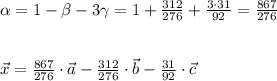
$\alpha =1- \beta -3\gamma =1+\frac{312}{276}+\frac{3\cdot 31}{92}=\frac{867}{276}\\\\\\\vec{x}=\frac{867}{276}\cdot \vec{a}-\frac{312}{276}\cdot \vec{b}-\frac{31}{92} \cdot \vec{c}$