Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 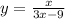 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)  при
при 
Если x = -5, то 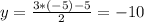
Если х= 3, то 
Значит, 
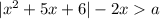
Анализируем: решение квадратного неравенства только вида 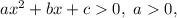 может содержать промежуток
может содержать промежуток 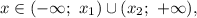 где
где 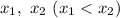 — корни квадратного уравнения
— корни квадратного уравнения 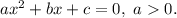
Раскроем модуль. Для этого воспользуемся правилом: 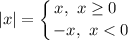
1) Пусть 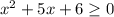
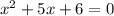
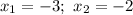 — абсциссы точек пересечения с осью абсцисс.
— абсциссы точек пересечения с осью абсцисс.
![x \in (-\infty; \ -3] \cup [-2; \ +\infty)](/tpl/images/1106/1316/ec0c2.png)
Тогда 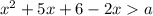
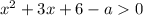
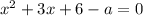
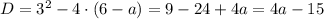
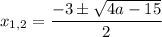
Решением исходного неравенства будет 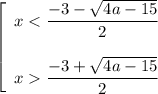
Следовательно, зная интервал 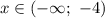 , определим значение параметра
, определим значение параметра  :
:
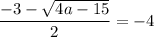
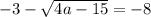
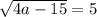
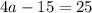
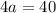
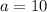
Таким образом, 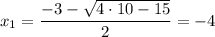 и
и 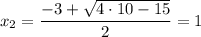
Решение: 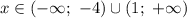
При пересечении условия модуля ![x \in (-\infty; \ -3] \cup [-2; \ +\infty)](/tpl/images/1106/1316/ec0c2.png) получаем окончательное решение:
получаем окончательное решение: 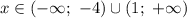 при
при 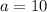
2) Если 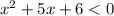 , то получаем
, то получаем 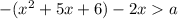 с отрицательным коэффициентом перед
с отрицательным коэффициентом перед 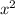 : это означает, что решением квадратного неравенства вида
: это означает, что решением квадратного неравенства вида 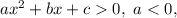 будет промежуток
будет промежуток 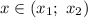 , где
, где 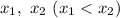 — корни квадратного уравнения
— корни квадратного уравнения 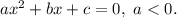 Этот случай нас не устраивает.
Этот случай нас не устраивает.
ответ: 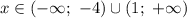 при
при 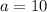
4x^2-14x+6=0(делим на 2)
2x^2-7x+3=0
Д=49-24=24
Х1=7+5/4=3
Х2=7-5/4=0,5
ответ:0,5;3