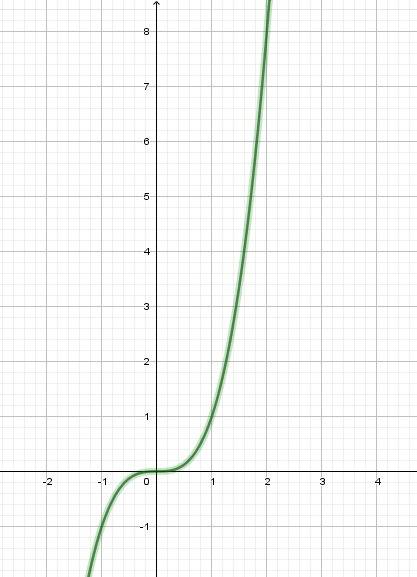
Точки построения графика: (0;0), (±1; ±1), (±2; ±8). График является нечетной.
Подставим координаты точки A(-5;125) в график уравнения, получим
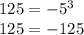
Поскольку равенство не верно, то график функции y = x³ не проходит через точку A(-5;125), т.е. точка не принадлежит графику y = x³
Подставим теперь координаты точки B(4;64), получим
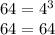
Поскольку равенство тождественно выполняется, то точка B принадлежит графику функции y = x³.
Подставим координаты точки C(-3;-27), имеем
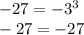
Раз равенство тождественно выполняется, то точка C(-3;-27) принадлежит графику функции y = x³
N-(m+k-f)=600.
Условимся ограничить поиск N в области трехзначных чисел. (Ясно что такое N единственно)
Ясно,что k<10 (10^3=1000) f<4 (4^6=
4096. Значит :k-f<=8. Тк 32^2>100,то наибольшее значение : m+k-f=39 для треxзначного N. Тогда область поиска N ограничено интервалом: 600 -639. Для любого N лежащего в этом интервале: m^2=25^2или m=24^2 ; k^3=8^3=512; f^6=2^6=64. Тогда можно сразу же найти N:(2 варианта) 1)N=600+(24+8-2)=630>25^2 значит m=25(противоречие) 2)N=600+(25+8-2)=631 (верно) ответ :631