I.
№1
Известно, что a < 3. Какой знак имеет следующее выражение:
а) 12a – 4; б) (a – 1)2(a – 3); в)
№2
Докажите, что если a > 5, то 3a – 7 > 8
II.
Решите неравенства : а) x – 3 > 0; б) 2x + 5 < 7
1) На координатной прямой показать множества решений неравенств:
x > 8; x < –5; x 2; x –2; x > 0,1
2) Найдите наименьшее целое значение, удовлетворяющее неравенству:
а) 2x + 13 > 57; б) 5x – 14 > 1; в) 3x + 8 > 2
3) Найдите наибольшее целое число, удовлетворяющее неравенству:
а) 5x – 6 < 14; б) 7x + 1 < –20
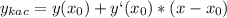
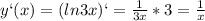
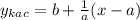
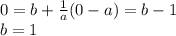

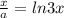

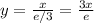
2) (м+4)^2-4(м+1)^2 = m^2 + 8m + 16 - 4m^2 - 8m - 4 = -3m^2 + 12
3) 3(2-у)^2+4(у-5)^2 = 3(4-2y+y^2) + 4(y^2-10y+25) = 12-4y+3y^2+4y^2-40y+100 =
=7y^2-44y+112
4) 5(3-5х)^2-5(3х-7)(3х+7) = 5(9-30x +25x^2) - 5(9x^2 - 21x + 21x -49) = =45-150x+125^2-45x^2+245 = 80x^2-150x+290
5) (а+1)^2+3(а-1)^2-5(а-1)(а+1)= a^2+2a+1+3(a^2-2a+1)-5(a^2-a+a-1) = =a^2+2a+1+3a^2-6a+3-5a^2+5= -a^2-4a+9
6) (х-1)^2-4(х+1)^2-6(х+1)(х-1)= x^2-2x+1-4(x^2+2x+1)-6(x^2+x-x-1)= =x^2-2x+1-4x^2-8x-4-6x^2+6=-9x^2-10x+3
2.Выполните действия:
1) ((3а+в)^2-(а+3в)^2)*2ав=(9a^2+6ab+b^2-a^2-6ab-9b^2)*2ab = =(8a^2-8b^2)*2ab=16a^3b-16ab^3
2) ((х^2+2х)^2+(2х^2-х)^2)/5х^2 = (x^4+4x^3+4x^2+4x^4-4x^3+x^2)/5x^2 = = (5x^4+5x^2)/5x^2 = 5x^2(x^2+1)/5x^2= x^2+1