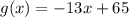 . Найдем значение
. Найдем значение  , при котором функция будет равна
, при котором функция будет равна 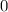 . Для этого приравняем саму функцию к
. Для этого приравняем саму функцию к 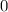 :
: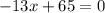
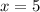 .
.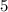 данная функция перескает ось абсцисс (OX). Так как у функции угловой коэффициент отрицательный (число -13), следует заключение, что функция убывает на всей области определения. Так как это линейная функция, то область определения у неё, вся числовая прямая. Отсюда следует, что функия - убывающая!
данная функция перескает ось абсцисс (OX). Так как у функции угловой коэффициент отрицательный (число -13), следует заключение, что функция убывает на всей области определения. Так как это линейная функция, то область определения у неё, вся числовая прямая. Отсюда следует, что функия - убывающая!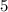 . Так как функция убывает, то отсюда получаем:
. Так как функция убывает, то отсюда получаем: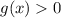 при
при 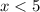
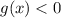 при
при  .
.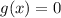 при
при 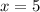
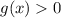 при
при 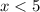
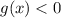 при
при 
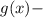 убывающая
убывающая
Решаем неравенство методом интервалов.
Находим нули функции у=(x+2)(x-1)(3x-7)
(x+2)(x-1)(3x-7)=0
Произведение нескольких множителей равно нулю, когда хотя бы один из них равен нулю.
х+2 = 0 или х - 1 = 0 или 3х - 7 = 0
х=-2 или х=1 или х=2 целых 1/3
Отмечаем точки на числовой прямой заполненным кружком (здесь это квадратные скобки) и расставляем знаки : - + - +
при х = -10 получаем (-10+2)(-10-1)(-30-7) <0
_ + _ +
[-2][1][2целых1/3]
поэтому на интервале, содержащем точку (-10),знак минус, далее знаки чередуем.
ответ: (−∞;−2]∪[1; 2 целых 1/3]