1. Верно у предыдущего ответчика x+y=10
x*y=24
2. А вот со второй чего-то возможно такое:
Вся работа =100%
Т.о Бригада 2 выполняет 100% за x дней
1-ая бригада выполняет за x+10 дней
Теперь нужно понять сколько %-ов выполняет 2 бригада относительно первой (ниже назовем это а), т.е пропорция:
x 100%
x+10 неизвестно скока %( назовем это а)
т.е а*x=100(x+10)
a=(100*(x+10))/x
Теперь рассмотрим суммарную работу бригад т.к они работают вместе, то работа будет равна 200% т.о:
x+a=200%
x+(100*(x+10))/x)=200
100(x+10)+x^2=200x тут x^2-это x в квадрате
100x+1000+x^2=200x
x^2-100x+1000=0
Из квадратного уравнения получаем корни:
x1=50+Под корнем(-100/2)^2-1000
x2=50-Под корнем(-100/2)^2-1000
x1=50+под корнем (2500-1000)
x2=50-под корнем (2500-1000)
x1=11,3
x2=88,7дней
Это два варианта дней за которые может сделать работу вторая бригада, но т.к две бригады делают за 12 дней, значит ответ 11,3 не верный, ибо одна бригада делать должна дольше, чем если они работают совместно.
Т.к 1-ая бригада работает x+10:
x=88,7+10=98,7 дней
ответ: 1-ая 98,7 дней, 2-ая 88,7дней
А если просто система уровнений нужна, то просто напиши:
x+(100*(x+10))/x)=200
x+10=x2
x-это дни первой бригады, а x2- второй
3 задача.
S=210 км
S1=2/3S=210*2/3=420/3=140км путь до остановки
S2=210-140=70км- путь после остановки
Первая часть пути 140=t*V t-время потраченное на эти 140 км, V-это постоянная скорость с которой ехал поезд эти 140км
Вторая чать пути 70=(t/2-10/60)(V+10) t/2-это потому что на проезд пути ему нужно в 2 раза меньше времени, чем на преодоление первой части, т.к расстояние в 2 раза меньше 140км в 2 раза меньше 70км. -10/60 это те потерянные минутына остановке, при чем их нужно перевести в часы. поэтому 10 минут делим на 60. V+10 т.к скорость на втором участке увеличилась на 10 км/ч.
В итоге система уравнений:
140=t*V
70=(t/2-10/60)(V+10)
Выражаем из первого уравнения t=140/V и подставляем его во второе:
70=(140/2V-10/60)(V+10)
70=(70/V-1/6)(V+10)
70=(((420-V)/6V)*(V+10)
420V=(420-V)(V+10)
420V=420V-V^2+4200-10V V^2-это V в квадрате
V^2+10V-4200=0
Дальше ищем корни квадратного уравнения:
V1,2=-10/2+-корень из(10/2)^2+4200=-5+-65
V1=60км
V2=-70км т.к расстояние не может быть отрицательным, то ответ V=60км.
По условию, нужно найти сумму несократимых дробей вида 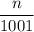 , это означает, что числа
, это означает, что числа 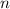 и 1001 - взаимно простые.
и 1001 - взаимно простые.
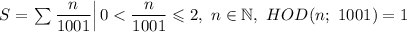
Разложим число 1001 на простые множители:
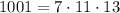
Рассмотрим искомую сумму, без учета условия о несократимости дроби 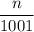 . Тогда получим:
. Тогда получим:
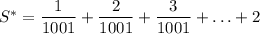
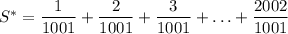
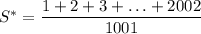
Задача сводится к нахождению суммы 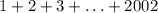 . Но мы помним, что на самом деле нас интересует сумма только тех чисел от 1 до 2002, которые являются взаимно простыми с числом 1001.
. Но мы помним, что на самом деле нас интересует сумма только тех чисел от 1 до 2002, которые являются взаимно простыми с числом 1001.
Найдем количество чисел от 1 до 2002, которые не являются взаимно простыми с числом 1001. По отношению к делимости на делители числа 1001, то есть на 7, 11, 13 все такие числа можно разделить на несколько групп:
- делятся на 7, но не делятся на 11, 13;
- делятся на 11, но не делятся на 7, 13;
- делятся на 13, но не делятся на 7, 11;
- делятся на 7, 11, но не делятся на 13;
- делятся на 7, 13, но не делятся на 11;
- делятся на 11, 13, но не делятся на 7;
- делятся на 7, 11, 13.
Количества таких чисел соответственно равно:
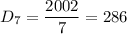
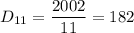
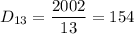
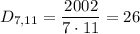
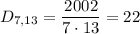
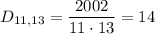
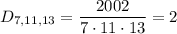
Найти итоговое количество чисел, не взаимно простых с 1001 можно по формуле включений-исключений, которая запишется в виде:
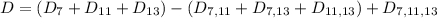
Формула подразумевает, что числа, имеющие два делителя из набора (7, 11, 13) были посчитаны среди первых трех слагаемых дважды, поэтому их необходимо один раз отнять. В свою очередь числа, делящиеся на каждое число набора (7, 11, 13) были посчитаны 3 раза со знаком "плюс" и 3 раза со знаком "минус", поэтому их необходимо отдельно прибавить.
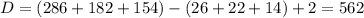
Тогда, количество чисел, взаимно простых с 1001:
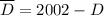
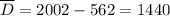
Составим следующую конструкцию. запишем числа от 1 до 2002 в столбик, а точнее для дальнейшего удобства - от 0 до 2002:
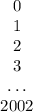
Во второй столбик запишем те же самые числа в обратном порядке:

Заметим, что сумма чисел в каждой строчке равна 2002.
Нетрудно понять, что два числа в одной строчке либо оба делятся на 7 (аналогично, на 11, на 13), либо оба не делятся. Поскольку 2002 делится на 7, то делимость первого числа в строчке гарантирует делимость второго числа и наоборот.
Тогда, вычеркнем из нашей таблицы 562 строчки, в которых первое число (а значит и второе тоже) не является взаимно простым с числом 1001. Вычеркнем также первую вс строчку (0-2002).
В таблице останется как было определено ранее 1440 чисел в каждом из столбцов. Поскольку мы знаем суммы чисел в каждой строчке, то легко определяется сумма всех чисел в таблице:
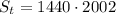
Заметим, что в таблице записан двойной набор тех чисел, что нам нужно сложить в числителе искомой величины.
Тогда:
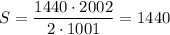
ответ: 1440
(3x+5-3x+1)(3x+5+3x-1)=10 (по формуле разности квадратов)
6*(6x+4)=10
36x+24=10
36x=-14
x=-(14/36)
вроде так