Решаем чисто аналитически:
Сначала найдем точки пересечения прямых (каждой с каждой), получим 3 точки, являющиеся вершинами треугольника.
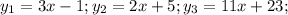
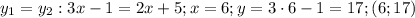 пусть это будет точка А.
пусть это будет точка А.
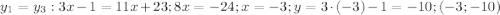 пусть это будет точка В.
пусть это будет точка В.
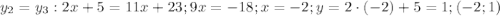 пусть это будет точка С.
пусть это будет точка С.
Итак, нашли координаты вершин треугольника.
Теперь вычислим расстояния между точками (от каждой до каждой)
Напомню, что расстояние между точками 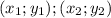
считается по формуле 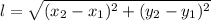
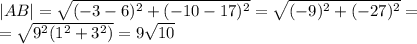
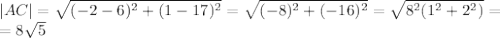
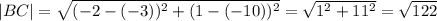
Известны длины всех сторон. По формуле Герона мы можем вычислить площадь. Но очень неприятно возиться с корнями, поэтому найдем лучше найти высоту треугольника, например, проведенной к основанию AC. Для этого надо вычислить коэффициенты уравнения прямой, содержащей эту высоту. Это можно сделать, исходя из того факта, что прямые BH (BH - высота к AC) и AC перпендикулярны, а значит, произведение их угловых коэффициентов равно -1.
Тогда уравнение прямой, перпендикулярной AC и проходящей через точку B, имеет вид
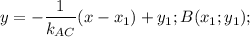
Надо понять, какое уравнение содержит точки A и C. Подставив в каждое координаты точек A и C, поймем, что это второе уравнение
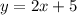
А учитывая, что B(-3;-10), получаем уравнение прямой, содержащей высоту к AC.
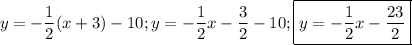
Теперь найдем координаты точки H - это пересечение прямой, содержащей высоту и прямой, содержащей точки A и C.
То есть
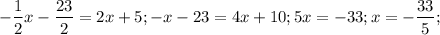
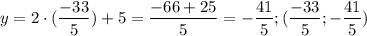
Вычислим длину высоты:
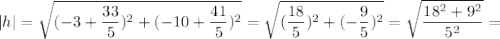
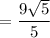
Площадь треугольника равна половине произведения основанию на высоту, проведенную к этому основанию. Считаем:
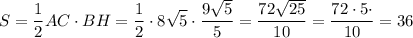
ответ: 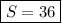
На этой странице я расскажу об одном популярном классе задач, которые встречаются в любых учебниках и методичках по теории вероятностей - задачах про бросание монет (кстати, они встречаются в части В6 ЕГЭ). Формулировки могут быть разные, например "Симметричную монету бросают дважды..." или "Бросают 3 монеты ...", но принцип решения от этого не меняется, вот увидите.
найти вероятность, что при бросании монеты
Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать "бросают 3 монеты" или "бросают монету 3 раза", результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).
Для задач о подбрасывании монеты существуют два основных метода решения, один - по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), а также его более сложный вариант с использованием комбинаторики, второй - по формуле Бернулли (на мой взгляд он даже легче первого, нужно только запомнить формулу). Рекомендую по порядку прочитать про оба метода, и потом выбирать при решении подходящий.
Объяснение: