пусть начинается последовательность с k (k > 0)
a1 = k
a2 = k + 1
an = k + n - 1
Sn = a1 + + an = n*k + n(n - 1)/2
2Sn = 2*n*k + n(n - 1) = 2nk + n² - n = n² + n(2k - 1)
получаем
221 < Sn < 234
442 < 2Sn < 468
442 < n² + n(2k - 1) < 468
а) n = 12
442 < 12² + 24k - 12 < 468
310 < 24k < 336
13 <= k < 14
да начальная 13
б) n = 13
442 < 13² + 26k - 13 < 468
286 < 26k < 312
11 < k < 12
нет между 11 и 12 нет целого числа
в) оценим максимум
n² + n < n² + n(2k - 1) < 468
21² + 21 = 462
n ≤ 21
n = 21
ищем целое k
k = 21
462 < 21² + 21(2k - 1) < 468
462 < 21² + 42k - 21 < 468
42 < 42k < 48
1 < k < 8/7 нет
k = 20
462 < 20² + 20(2k - 1) < 468
462 < 20² + 40k - 20 < 468
82 < 40k < 86
41/20 < k < 43/20 нет
k = 19
462 < 19² + 19(2k - 1) < 468
462 < 19² + 38k - 19 < 468
120 < 38k < 126
60/19 < k < 63/19 нет
k = 18
462 < 18² + 18(2k - 1) < 468
462 < 18² + 36k - 18 < 468
156 < 36k < 162
78/18 < k < 81/18 нет
k = 17
462 < 17² + 17(2k - 1) < 468
462 < 17² + 34k - 17 < 468
190 < 34k < 196
85/17 < k < 88/17 нет
k = 16
462 < 16² + 16(2k - 1) < 468
462 < 16² + 32k - 16 < 468
222< 32k < 228
6.9375 < k < 7.125 УРА НАШЛИ n=21 k=16
![sin2x + 2sinx = 1 + cosx\\2sinxcosx+2sinx=1+cosx\\2sinx(1+cosx) = 1 + cosx\\(2sinx-1)(1+cosx) = 0\\sinx = \frac{1}{2} = x = (-1)^n\frac{\pi}{6} + \pi n, n \in Z\\ cosx = -1 = x = \pi + 2\pi m, m \in Z\\x \in [-4;-3]\\-4 < (-1)^n\frac{\pi}{6} + \pi n < -3\\-24 < (-1)^n\pi+6\pi n < -18\\](/tpl/images/1359/4064/d08e0.png)
Подставляем n = 0 - неравенство не выполнено. n = 1 - неравенство не выполнено. Следовательно, при n ≥ 0 решений не будет, т.к. (-1)^n + 6n - функция возрастающая.
Пусть n = -1, тогда выражение 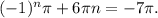 Так как 3.14 < π < 3.15, то
Так как 3.14 < π < 3.15, то
-22.05 < -7π < -21.98. Очевидно, оно попадает на промежуток (-24; -18). Значит, при n = -1 решение есть на данном отрезке. Подставим n = -1 в серию корней:
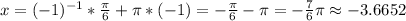
Такими же рассуждениями приходим к тому, что n ≤ -2 так же не являются решениями.
Теперь рассмотрим вторую серию корней:
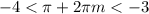
Тут совсем все просто: при m = 0, очевидно, неравенство не выполнено. При m = 1 так же. Так как выражение 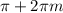 при возрастании m увеличивается, то и m ≥ 2 также не подходят.
при возрастании m увеличивается, то и m ≥ 2 также не подходят.
Пусть m = -1, тогда:

Очевидно, что это так. Подставляя m = -2 понимаем, что число меньше -4.
Вопросы ниже в комменты.
ответ: 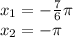
a; b = a + 1; c = a + 2.
c^2 - a^2 = 4b
(a+2)^2 = a^2 + 4(a+1)
a^2 + 4a + 4 = a^2 + 4a + 4
4a + 4 = 4a + 4
4 = 4
0 = 0
Вывод: не зависит от выбора а.
Для любого натурального числа a и двух чисел b = a + 1 и c = a +2 выполняется равенство выше.
Пример : 1,2,3
3*3 - 1 = 4 * 2
9 - 1 = 8
8 = 8