Теорема (о сумме углов выпуклого многоугольника)
Сумма внутренних углов выпуклого многоугольника равна 180º(n-2). (n — количество сторон многоугольника).
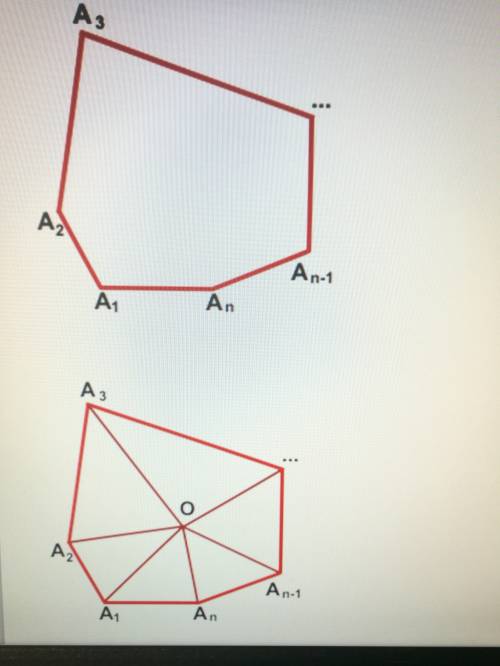
(смотри верхний рисунок)
— выпуклый n -угольник.
Обозначим внутри многоугольника произвольную точку O.
Соединим точку O с вершинами многоугольника.
(смотри нижний рисунок)
Получили n треугольников.
Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.
То есть в данном случае у нас 6-угольник, имеем 6 треугольников, сумма углов которых 6*180 и минус 2*180 – сумма углов при вершине. Получается 180*(6 – 2) = 720 гр.
Так как сумма углов при вершине O составляет 360º, то сумма углов многоугольника равна сумме углов n треугольников минус 360º.
а) 3х² - 17х + 10 = 0 ; б) х² - 6х + 6 = 0;
Объяснение:
х² + рх + q = 0
По теореме Виета
х₁ + х₂ = -р
х₁ · х₂ = q
а) х₁ = 2/3; х₂ = 5
х₁ + х₂ = 2/3 + 5 = 17/3 ⇒ p = -17/3
х₁ · х₂ = 2/3 · 5 = 10/3 ⇒ q = 10/3
х² - 17х/3 + 10/3 = 0
или
3х² - 17х + 10 = 0
б) х₁ = 3 - √3; х₂ = 3 + √3;
х₁ + х₂ = 3 - √3 + 3 + √3 = 6 ⇒ p = -6
х₁ · х₂ = (3 - √3) · (3 + √3) = 9 - 3 = 6 ⇒ q = 6
х² - 6х + 6 = 0