1)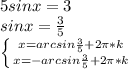
2)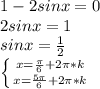
3)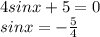
нет ответа т.к. -5/4 <-1
4) 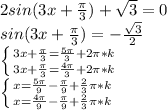
5)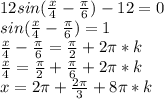
6)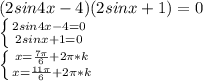
7)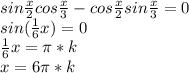
8)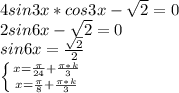
Объяснение:
По условию a^2 + 2cd + b^2 = k^2 и c^2 + 2ab + d^2 = m^2, где k и m - натуральные. Тогда 2cd = k^2 - a^2 - b^2 и 2ab = m^2 - c^2 - d^2. Составим квадраты сумм a + b и c + d: (a + b)^2 = a^2 + b^2 + 2ab = a^2 + b^2 + m^2 - c^2 - d^2 и (c + d)^2 = c^2 + d^2 + 2cd = c^2 + d^2 + k^2 - a^2 - b^2. Теперь составим их сумму: (a + b)^2 + (c + d)^2 = a^2 + b^2 + m^2 - c^2 - d^2 + c^2 + d^2 + k^2 - a^2 - b^2 = m^2 + k^2 => (a - b)^2 = k^2, (c - d)^2 = m^2. Тогда a^2 + 2cd + b^2 = (a + b)^2 = a^2 + 2ab + b^2 => 2ab = 2cd => ab = cd. Полученное условие должно соблюдаться и нам подойдут, к примеру, числа ab = cd = 6 => 1*6 = 2*3 => a=1, b=6, c=2, d=3. Действительно, a^2 + 2cd + b^2 = 1^2 + 2*2*3 + 6^2 = 1 + 12 + 36 = 49 = 7^2 и c^2 + 2ab + d^2 = 2^2 + 2*1*6 + 3^2 = 4 + 12 + 9 = 25 = 5^2.
ответ: a =1, b = 6; c = 2, d = 3.
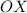 , а так же, что есть формула для нахождения вершины параболы
, а так же, что есть формула для нахождения вершины параболы 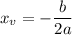
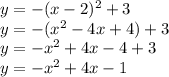
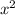 отрицательный, значит ветви рисуем вниз.
отрицательный, значит ветви рисуем вниз.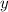 к нулю.
к нулю.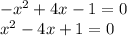
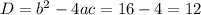
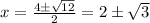
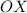
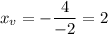 Подставляем в квадратное уравнение и находим
Подставляем в квадратное уравнение и находим 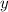 .
. 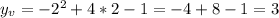
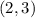 является вершиной параболы. ветви вниз. и в точках
является вершиной параболы. ветви вниз. и в точках 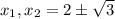 проходит через ось
проходит через ось 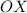
1) 5sinx =3 ⇔ sinx = 0,6 ⇒ x = (-1)ⁿarcsin(0,6) +πn , n ∈ ℤ .
2) 1 - 2sinx = 0⇔ sinx = 1/2 ⇒ x = (-1)ⁿπ/6 +πn , n ∈ ℤ .
3) 4sinx +5 =0 ⇔ sinx = -1,25 ⇒ x ∈ ∅ . не имеет решения | sinx | ≤ 1
4) 2sin(3x +π/3) + √3 =0 ⇔sin(3x +π/3) = -(√3) /2 ⇒
3x+ π/3 = (-1) ⁿ⁻¹ π/3 + πn ⇔ (совокупность _ИЛИ )
[ 3x+ π/3 = - π/3 + π*2k ; 3x+ π/3 = π/3 + π*(2k+1) , k ∈ ℤ ⇔
[ x = - 2π/9 + (2π/3)k ; x= (π/3)(2k+1) , k ∈ ℤ
5) 12sin(x/4 -π/6) -12 =0 ⇔sin(x/4 -π/6) =1 ⇒ x/4 -π/6 =π/2 +2πk ,k ∈ ℤ ⇔
x = 8π/3 +8πk ,k ∈ ℤ
6) (2sin4x - 4)(2sinx+1) =0 ⇔ (sin4x -2)(sinx +1/2) = 0 ||sin4x ≠2 || ⇔
sinx +1/2 =0 ⇔sinx = -(1/2) ⇒ x =(-1) ⁿ⁻¹ *(π/6) + πn , n ∈ ℤ
7) sin(x/2)cos(x/3) -cos(x/2)sin(x/3) =0⇔sin(x/2 - x/3) =0 ⇔sin(x/6) =0 ⇒
x/6 =πn , n ∈ ℤ ≡ x = 6πn , n ∈ ℤ
8) 4sin3x*cos3x - √2 =0 ⇔ 2sin(2*3x) - √2 =0 ⇔sin(6x) =(√2)/2 ⇔
6x =π/4 +πn , n∈ℤ ⇔ x = π/24 +(π/4)*n , n∈ℤ