ответ: Уравнение эллипса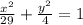 
; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)
Объяснение:
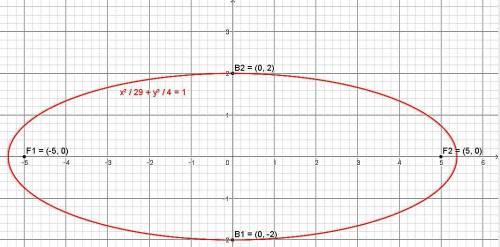
Дан эллипс: F₁ =(-5;0); F₂ =(5;0) и B₁=(0;-2); B₂=(0;2). Напишите уравнение эллипса, найти оси и эксцентриситет
фокусное расстояние эллипса с = 5 (от точки F до точки О)
малая полуось b = 2
большая полуось а находится из соотношения
а² = b² + c²
a² = 2² + 5² = 4 + 25 = 29
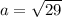
уравнение эллипса:
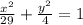
- каноническое уравнение эллипса
Оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии.
Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .
ε = с/ a = 5/√(29)
y = 3Cosx + 2Sin²x - 1
Найдём производную :
y' = (Cosx)' + 2(Sin²x)' - 1' = - 3Sinx + 4SinxCosx
Приравняем производную к нулю :
- 3Sinx + 4SinxCosx = 0
Sinx(- 3 + 4Cosx) = 0
Sinx = 0
- 3 + 4Cosx = 0
Cosx = 0,75
Если Sinx = 0 , то Cosx = ± 1
1) Sinx = 0 ⇒ Cosx = - 1 ⇒
y = 3 * (- 1) + 2 * 0 - 1 = - 4 - наименьшее
2) Sinx = 0 ⇒ Cosx = 1 ⇒
y = 3 * 1 + 2 * 0 - 1 = 2
3) Cosx = 0,75 ⇒ Sin²x = 1 - Cos²x = 1 - 0,75² = 1 - 0,5625 = 0,4375
y = 3 * 0,75 + 2 * 0,4375 - 1 = 2,25 + 0,875 - 1 = 2,125 - наибольшее
ответ : наименьшее - 4 , наибольшее 2,125