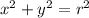, задаёт окружность радиуса r
Что бы задать лучи, используем несколько функций вида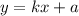 
При a = 0, все прямые, задаваемые уравнениями вида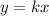 
, будут проходить через точку пересечения координатных осей.
Возьмём 5 прямых, которые будут иметь угол с осью Ох, соответственно, в 0, 30, 60,120, 150 градусов. Этим углам соотвествуют следующие значения углового коэффициента k: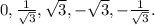 
Под углом 90 градусов будет падать прямая x = 0.
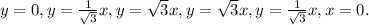
Осталось вырезать у этих прямых отрезки, которые лежат внутри окружности. Для этого найдём точки пересечения этих прямых и окружности.
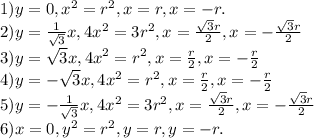
Тогда:
![(x^2+y^2 = r^2) \cup (y=0, x \in (-\infty, -r]\cup[r, +\infty)) \cup\\ (y=\frac{1}{\sqrt{3}}x, x \in (-\infty, -\frac{\sqrt{3}r}{2}]\cup[\frac{\sqrt{3}r}{2}, +\infty))\cup\\(y=\sqrt{3}x, x \in (-\infty, -\frac{r}{2}]\cup[\frac{r}{2}, +\infty))\cup\\(y=-\sqrt{3}x, x \in (-\infty, -\frac{r}{2}]\cup[\frac{r}{2}, +\infty)\cup\\(y=-\frac{1}{\sqrt{3}}x, x \in (-\infty, -\frac{\sqrt{3}r}{2}]\cup[\frac{\sqrt{3}r}{2}, +\infty))\cup\\(x=0, y \in (-\infty, -r]\cup[r, +\infty))](/tpl/images/0155/2774/da10b.png)
Так как полный оборот(360 градусов) на еденичной окружности равен 2пи, а половинный( 180 градусов) равен пи, то 5п, можно упростить до п, так как это два полных оборота плюс один полуоборот( 2п+2п+п).
Получим: tg(pi/2 - a), по формулам приведения увидем, что tg(pi/2 - a)=сtg(a)
У формул приведения есть своя логика, в данном случае такая, если оборот равен пи/2, то есть 90 градусов или 3пи/2, то есть270 градусов, то синус меняется на косинус и наоборот, а тангенс меняется на катангенс и наоборот, при Пи(180 градусов) или нуле, остаётся прежним.
Далее смотрим на то, положителен или отрицателен в данном случае тангенс в этой четверти, Так как пи( 180 градусов), то п-а(то есть малая часть), будет находиться во второй четверти,а тангенс там положительный, соответственно знак остаётся таким же. елси бы был отрицательный, то взяли бы минус ctg a.
Вот такие аладушки. :)