1) 12 шаг/мин * 80 см = 960 см/мин = 9,6 (м/мин) - скорость первого судьи; 2) 10 шаг/мин * 80 см = 800 см/мин = (8 м/мин) - скорость второго судьи; 3) 9,6 м/мин + 8 м/мин = 17,6 (м/мин) - скорость сближения; 4) 17,6 м/мин * 20 мин = 352 (м) - расстояние между пунктами. ответ: 352 м.
1) 12 шаг/мин * 80 см = 960 (см/мин) - скорость первого судьи; 2) 960 см * 20 мин = 19 200 см = 192 (м первый судья до встречи; 3) 10 шаг/мин * 80 см = 800 см/мин - скорость второго судьи; 4) 800 см/мин * 20 мин = 16 000 см = 160 (м второй судья до встречи; 5) 192 м + 160 м = 352 (м) - расстояние между пунктами. ответ: 352 м.
1) 12 шаг/мин * 80 см = 960 см/мин = 9,6 (м/мин) - скорость первого судьи; 2) 10 шаг/мин * 80 см = 800 см/мин = (8 м/мин) - скорость второго судьи; 3) 9,6 м/мин + 8 м/мин = 17,6 (м/мин) - скорость сближения; 4) 17,6 м/мин * 20 мин = 352 (м) - расстояние между пунктами. ответ: 352 м.
1) 12 шаг/мин * 80 см = 960 (см/мин) - скорость первого судьи; 2) 960 см * 20 мин = 19 200 см = 192 (м первый судья до встречи; 3) 10 шаг/мин * 80 см = 800 см/мин - скорость второго судьи; 4) 800 см/мин * 20 мин = 16 000 см = 160 (м второй судья до встречи; 5) 192 м + 160 м = 352 (м) - расстояние между пунктами. ответ: 352 м.
Пусть - канонический базис в
- канонический базис в 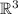 .
.
Тогда матрицу перехода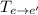 можно найти следующим образом:
можно найти следующим образом:
Если записать блочную матрицу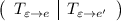 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 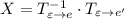
Матрицу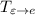 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей 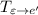 .
.
В итоге необходимо получить вид следующей матрицы:
следующей матрицы:
Вычтем первую строку из второй и третьей:
Вычтем из первой строки 2 третьих и поменяем их местами:
Вычтем из третьей строки вторую:
Прибавим ко второй строке 2 третьих и вычтем из первой третью:
Делим вторую строку на 3:
Прибавляем в первой строке 2 вторых: