Запишите в виде квадрата двучлена: 4m^2-4m+1 2)Запишите в виде квадрата двучлена: 1/4x^2-2/15x^2y^2+1/25y^4 - id1149508520211103 от Alenka267 03.11.2021 02:19

Question

Алгебра: Запишите в виде квадрата двучлена: 4m^2-4m+1 2)Запишите в виде квадрата двучлена: 1/4x^2-2/15x^2y^2+1/25y^4 3)Представьте в виде квадрата двучлена выражение: 9a^2+42a+49 4)Из данных выражений отметьте то, которое можно представить в виде квадрата двучлена. 9a^2+4-12a 2c^2+6c+3 9x^2-6x+4 16b^2+4b+1 5)Замените символ * в выражении 16-40+* таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена. Вычислите значение полученного выражения при a= -3/5

Alenka267 · Accepted Answer

Если прямая перпендикулярно плоскости, то ее направляющий вектор является нормальным вектором плоскости.

1)Уравнение плоскости через нормальный вектор: Ax+By+Cz+D=0

, где A, B, C - координаты нормального вектора плоскости N(A,B,C).
Уравнение данной плоскости 2x-3y+4z-3=0

⇒ N(2,-3,4).

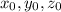2)Уравнение прямой через точку направляющий вектор: $\frac{x-x_{0}}{l}=\frac{y-y_{0}}{m}=\frac{z-z_{0}}{n}$ , где $x_{0},y_{0},z_0}$ - координаты точки M( 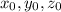$x_{0},y_{0},z_0}$ ), через которую проходит прямая, l,m,n

- координаты направляющего вектора S( l,m,n

).
По условию S( l,m,n

) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).

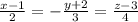
3)Готовое уравнение прямой: $\frac{x-1}{2}=-\frac{y+2}{3}=\frac{z-3}{4}$

MOGZ ответил