Дано: прямоугольный Δ
a; b - катеты
S=90 см²
S₁+S₂ = а²+b² =369 см₂
a-? b-?
Решение
1) Первое уравнение получаем из условия:
а²+b² = 369
2) Площадь прямоугольного треугольника равна половине произведения катетов, получаем второе уравнение:
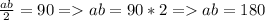
3) Решаем систему: (a>0; b>0)
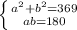
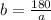
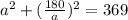
a≠0
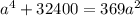
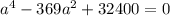
Замена: а²=t ( t > 0)
Решаем уравнение:
t² - 369t + 32400 = 0
D = 369² - 4·1·32400 = 136161 - 129600 = 6561 = 81²
t₁ = (369-81)/2 = 144
t₂ = (369+81)/2 = 225
Обратная замена:
При t₁ = 144 => a² = 144 => a₁ = - √144 = - 12 < 0
a₂ = √144 = 12 > 0
При t₂ = 225 => a² = 225 => a₃ = - √225 = - 15 < 0
a₄ = √225 = 15 > 0
Зная а₁=12 и а₂ = 15, найдем b
b₁ = 180/12 = 15
b₂ = 180/15 = 12
Получаем два решения взаимозаменяемых:
а=12; b=15
а=15; b=12
ответ: 12 см; 15 см - катеты
Объяснение:
Графиком зависимости является прямая, проходящая через точки
А (1; 2) и B(-1; 4).
а) Постройте эту прямую.
Существует формула составления уравнения прямой по координатам двух точек:
(х - х₁)/(х₂ - х₁) = (у - у₁)/(у₂ - у₁)
х₁=1 х₂= -1
у₁=2 у₂=4
Подставляем значения в формулу:
(х-1)/(-1-1)=(у-2)/(4-2)
(х-1)/(-2)=(у-2)/(2) перемножаем крест-накрест:
2(х-1)=(-2)(у-2)
2х-2= -2у+4
2у=4+2-2х
2у=6-2х
у=(6-2х)/2
у=3-х уравнение прямой, которую нужно построить.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 4 3 2
б) Найдите координаты точек ее пересечения с осями
координат.
Прямая пересекает ось Ох при у=0:
у=3-х
0=3-х
х=3
Координаты точки пересечения графиком оси Ох (3; 0)
Прямая пересекает ось Оу при х=0:
х=0
у=3-х
у=3-0
у=3
Координаты точки пересечения графиком оси Оу (0; 3)
в) Укажите координаты нескольких точек графика, которые лежат в I, II и II| координатных четвертях.
I четверть: (2; 1) (1; 2)
II четверть: (-1; 4) (-3; 6) (-4; 7)
III четверть: график данной прямой не проходит по этой четверти.