Алгебра: Решите задачу С подробным решением Задача в фото ниже

Решите задачу

С подробным решением
Задача в фото ниже

👇

Увидеть ответ

Открыть все ответы

Ответ:

ЕсенжоловаЛяззат

07.06.2020

$3; \quad 10; \quad 3;$

Объяснение:

6) Так как произведение корней принимает положительное значение, то и сами корни принимают положительные значения ⇒ подкоренные выражения также положительны.

ОДЗ:

$\left \{ {{x+10} \atop {x+60}} \right. \Leftrightarrow \left \{ {{x-1} \atop {x-6}} \right. \Leftrightarrow x -1 \Leftrightarrow x \in (-1; +\infty);$

$\sqrt{x+1}\sqrt{x+6}=6;$

$(\sqrt{x+1}\sqrt{x+6})^{2}=6^{2};$

$(\sqrt{x+1})^{2} \cdot (\sqrt{x+6})^{2}=36;$

(x+1)(x+6)=36;

$x^{2}+6x+x+6-36=0;$

$x^{2}+7x-30=0;$

$\left \{ {{x_{1}+x_{2}=-7} \atop {x_{1} \cdot x_{2}=-30}} \right. \Leftrightarrow \left \{ {{x_{1}=-10} \atop {x_{2}=3}} \right. ;$

Корень x₁ не удовлетворяет ОДЗ.

7) Знаменатель дроби не равен нулю ⇒ подкоренное выражение строго больше 0. Подкоренное выражение правой части уравнения также строго больше 0, поскольку, в противном случае, значение числителя равно 0, отсюда выходит, что "х" принимает отрицательное значение, что противоречит ОДЗ подкоренного выражения знаменателя дроби.

ОДЗ:

$\left \{ {{x-20} \atop {3x+20}} \right. \Leftrightarrow \left \{ {{x2} \atop {x-\frac{2}{3}}} \right. \Leftrightarrow x2 \Leftrightarrow x \in (2; +\infty);$

$\frac{x+6}{\sqrt{x-2}}=\sqrt{3x+2};$

$x+6=\sqrt{x-2} \cdot \sqrt{3x+2};$

$(x+6)^{2}=(\sqrt{x-2} \cdot \sqrt{3x+2})^{2};$

$x^{2}+12x+36=(\sqrt{x-2})^{2} \cdot (\sqrt{3x+2})^{2};$

$x^{2}+12x+36=(x-2)(3x+2);$

$x^{2}+12x+36=3x^{2}+2x-6x-4;$

$x^{2}-3x^{2}+12x-2x+6x+36+4=0;$

$-2x^{2}+16x+40=0;$

$x^{2}-8x-20=0;$

$\left \{ {{x_{1}+x_{2}=8} \atop {x_{1} \cdot x_{2}=-20}} \right. \Leftrightarrow \left \{ {{x_{1}=-2} \atop {x_{2}=10}} \right. ;$

Корень x₁ не удовлетворяет ОДЗ.

8) ОДЗ:

$2x-1\geq0;$

$2x\geq1;$

$x\geq\frac{1}{2};$

$\sqrt{x^{2}+2x+10}=2x-1;$

$(\sqrt{x^{2}+2x+10})^{2}=(2x-1)^{2};$

$x^{2}+2x+10=4x^{2}-4x+1;$

$x^{2}-4x^{2}+2x+4x+10-1=0;$

$-3x^{2}+6x+9=0;$

$x^{2}-2x-3=0;$

$\left \{ {{x_{1}+x_{2}=2} \atop {x_{1} \cdot x_{2}=-3}} \right. \Leftrightarrow \left \{ {{x_{1}=-1} \atop {x_{2}=3}} \right. ;$

Корень x₁ не удовлетворяет ОДЗ.

4,7(66 оценок)

Ответ:

AngelinaGi2006

07.06.2020

Мы делаем предположение, что то, что нам дано неверно, к примеру:

Доказать иррациональность числа 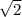$\sqrt{2}$

Допускаем противное, что число 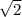$\sqrt{2}$ - рациональное, после чего уже доказываем что наше предположение не верно, в примере с корнем:

Любое рациональное число можно представить как несократимую дробь, где числитель - целое число, а знаменатель - натуральное

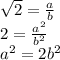
$\sqrt{2}=\frac{a}{b}\\2=\frac{a^{2}}{b^{2}} \\a^{2} = 2 b^{2}\\$

Отсюда следует, что 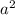$a^{2}$ чётно, значит, чётно и a; следовательно, 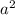$a^{2}$ делится на 4, а значит, 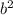$b^{2}$ и 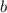тоже чётны. Полученное утверждение противоречит несократимости дроби 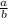$\frac{a}{b}$ . Это противоречит изначальному предположению и 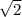$\sqrt{2}$ - иррациональное число.