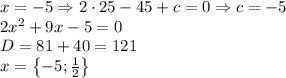
Объяснение:
Расставим порядок действий:
Первое и второе действие в скобках, третье - деление.
Решаем первое действие.
Для начала вспомним, что для того, чтобы вычесть или сложить алгебраические дроби, необходимо знаменатели дробей разложить на множители и привести их к общему знаменателю.
В знаменателе первой дроби мы можем вынести за скобку x.
Получим:
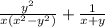
В знаменателе первой дроби у нас появилась формула разности квадратов. Развернем эту формулу и получим:
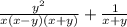
Теперь мы можем смело привести эти дроби к общему знаменателю.
Во второй дроби есть x + y, давайте-ка домножим вторую дробь на те множители, которые есть только у первой дроби, т.е., на x и на (x - y)
Имеем:
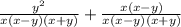
Справка: мы домножили на множители и числитель, и знаменатель.
Раскроем скобки во второй дроби и сложим числители дробей:
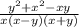
Второе действие:
Делаешь все то же самое. ответ ко второму действию: 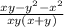 или
или 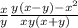
Третье действие:
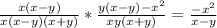
Объяснение:
Просто так я списать тебе не дам. Я объясню тебе первый пример, а следующие примеры, будь добр - сам.
Пример №1.
x - 3,8 при x = 1,2; 3,8; -4 1/3
В таких случаях нам надо подставить данные нам числа под x.
Подставляем:
1,2 - 3,8 = -2,6 (Я же надеюсь, ты умеешь обращаться с отрицательными числами?)
Подставим следующее значение:
3,8 - 3,8 = 0.
Последнее будет по-сложнее, но я надеюсь, что дроби, с которыми ты должен был познакомиться на уроках математики в 6 классе, ты знаешь.
Итак, подставляем:
-4 1/3 - 38/10 = 0
Почему 3,8 превратилось в 38/10? Потому что 38 при делении на 10 даст нам 3,8, то есть, мы 3,8 перевели в обыкновенную дробь для удобства.
Переведем -4 1/3 в неправильную дробь:
4 * 3 + 1 = 13.
Получаем:
-13/3 - 38/10
Приводим дроби к общему знаменателю 30.
У первой дроби будет доп.множитель 10, так как при делении общ.знам 30 на знам.первой дроби 3 будет 10.
У второй дроби доп.множитель - 3.
Умножаем числители на доп.множители и получаем:
39/30 - 114/30 = -84/30 = -2 24/30
Задача решена.