ответ: V1=24 км/ч, V2= 40 км/ч.
Объяснение:
Пусть скорость второго равна х км/ч.
Тогда первого будет х+16 км/ч.
Первый затратит на путь в 120 км - 120/(х+16) часов,
А второй - 120/х часов.
Разность во времени 2 часа.
Составим уравнение:
120/х - 120/(х+16)=2;
Найдем общий знаменатель: х(х+16), дополнительные множители:
(х+16, х и х(х+16)) .
120(х+16)-120х=2х(х+16);
120х+1920-120х=2х²+32х;
2х²+32х-1920=0; [:2]
x²+16x-960=0;
По теореме Виета
х1+х2=-16; х1*х2=960;
х1=24; х2= -40 - не соответствует условию задачи.
V2=24 км/ч - скорость второго мотоциклиста.
V1=x+16=24+16=40 км /ч
8
Объяснение:
Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то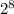 
сравнимо с 1 по модулю 15.
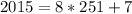
Тогда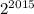 
можно записать в виде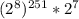 
Поскольку мы выяснили, что 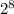сравнимо с 1 по модулю 15, то 
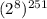также сравнимо с 1 по модулю 15.
Остаётся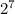 
, которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
То есть можем записать: 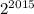≡ ≡ 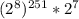≡ 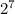8 mod 15
Это значит, что остаток равен 8.
Прикрепила файл
Объяснение:
1. Чертим координатную прямую
2. Обозначаем числа
3. Если промежуток или неравенство строгое (круглые скобки, знак > или <), то точка не входит в неравенство, остаётся незакрашенной
4. Если промежуток или неравенство нестрогое (квадратные скобки, знак
), то точка входит в неравенство, закрашиваем её