Объяснение:
Надо считать лучше и проблем не будет:
15(q-1)=(q^5)-1,15(q-1)=(q-1)(q⁴+q³+q²+q+1), (q-1)(q⁴+q³+q²+q+1)-15(q-1)=(q-1)(q⁴+q³+q²+q-14)=0
учитывая целочисленность прогрессии, получим q-1=0, q=q1=1
Для справки: q⁴+q³+q²+q-14=0 решается, например, методом Декарта -Эйлера и получается два действительных корня: q2≈1.5707, q3≈-2.1534 и два мнимых корня: q4≈-0.2087-2.0238i, q5≈-0.2087+2.0238i
Формула сложной процентной ставки: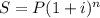 
, где S - наращенная сумма, P - первоначальная сумма вклада, i - процентная ставка, n - срок ссуды;
Само решение:
Пусть клиент сначала положил x грн в банк, тогда через год он получит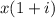 
грн и получил он прибыль 100 грн, т.е. 
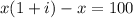откуда 
К общей сумме он добавил 400 грн на год свои сбережения в банке, то на следующий год он получит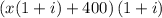 
грн, что по условию вклад вместе с процентами составил 1650 грн.
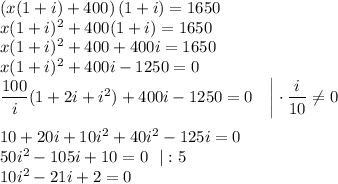
Решаем как квадратное уравнение через дискриминант
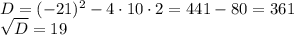
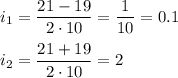
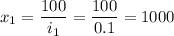грн - начальная сумма вклада
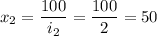грн - не подходит условию, так как клиент положил несколько 100 гривневых купюр
ответ: начальная сумма вклада 1000 грн с 10% годовыми.
ответ 5 тысяч девятьсот девяноста девять