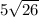
Решение системы уравнений х₁=5 х₂= -6 х₃=6
у₁=1 у₂= -10 у₃=2
Объяснение:
Решить систему уравнений
(x-5y)(x²-36)=0
x-y=4
Выразим х через у во втором уравнении:
х=4+у
Первые скобки приравняем к нулю, как один из множителей, дающих в результате ноль:
x-5y=0
Подставим выраженное х через у:
4+у-5у=0
4-4у=0
-4у= -4
у= -4/-4
у₁=1
Теперь подставляем значение у в уравнение первых скобок и вычисляем х:
x-5y=0
х=5у
х=5*1
х₁=5
Теперь приравняем к нулю вторые скобки, как один из множителей, дающих в результате ноль:
x²-36=0
x²=36
х₂,₃=±√36
х₂= -6
х₃=6
x-y=4
-у=4-х
у=х-4
у₂=х₂-4
у₂= -6-4
у₂= -10
у₃=х₃-4
у₃=6-4
у₃=2
Решение системы уравнений х₁=5 х₂= -6 х₃=6
у₁=1 у₂= -10 у₃=2
Объяснение:
1) в сосуде была наполнена часть,назовем ее Х и долили а
тогда Х+а=1/8, если отлили а от Х то в сосуде
Х-а=3/20 складываем почленно уравнения
Х+а+Х-а=1/8+3/20 Первую дробь домножаем на 5 ,а вторую на 2
2Х=11/40
х=11/80
В начале в сосуде было налито 11/80 всего объема.
2) 1/5 НЕ заполнена водой. Значит долить надо именно эту недорстающую часть! Заполнена водой 4/5 всего объема. Значит ищем отношение недостающей части к заполненому объему
1/5:4/5=(1*5)/(4*5)= 1/4. Значит долить надо 1/4 заполненого объема.