Объяснение:
При n=1 верность неравенства очевидна.
При n=2, получаем известное верное неравенство, оно нам понадобится.
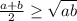
Теперь докажем, что из верности неравенство верно для n=m, следует его верность для n=2m.
В самом деле, пусть неравенство верно для n=m. Нам нужно доказать, что тогда верно и неравенство
![\frac{a_1+a_2+...+a_m+a_{m+1}+...+a_{2m}}{2m} \geq \sqrt[2m]{a_1a_2...a_{2m}}](/tpl/images/1381/5136/47de1.png)
Так как неравенство верно для n=m (по индуктивному предположению), можем записать такие два неравенства:
![\frac{a_1+a_2+...+a_m}{m} \geq \sqrt[m]{a_1a_2...a_{m}} \\\frac{a_{m+1}+a_{m+2}+...+a_{2m}}{m} \geq \sqrt[m]{a_{m+1}...a_{2m}} \\](/tpl/images/1381/5136/f3eff.png)
Теперь сложим эти неравенства и разделим обе части полученного на 2. Получится вот такое неравенство:
![\frac{a_1+a_2+...+a_{2m}}{2m} \geq \frac{\sqrt[m]{a_1a_2...a_{m}}+\sqrt[m]{a_{m+1}...a_{2m}}}{2}](/tpl/images/1381/5136/3b971.png)
Но использовав неравенство для n=2 получаем:
![\frac{\sqrt[m]{a_1a_2...a_{m}}+\sqrt[m]{a_{m+1}...a_{2m}}}{2} \geq \sqrt{\sqrt[m]{a_1a_2...a_{m}}\sqrt[m]{a_{m+1}...a_{2m}}} =\sqrt[2m]{a_1a_2...a_{2m}}](/tpl/images/1381/5136/b1700.png)
Тогда и подавно
![\frac{a_1+a_2+...+a_{2m}}{2m} \geq \sqrt[2m]{a_1a_2...a_{2m}}](/tpl/images/1381/5136/a1600.png)
А теперь, следуя за Коши (который как раз первым доказал это неравенство), заметим, что из доказанного выше следует, что если неравенство верно для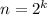 
(где k - натуральное), то оно верно и для 
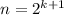. Действительно, чтобы доказать это, достаточно положить 
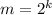, тогда 
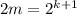и неравенство также верно. А так как неравенство верно для n=2, то по индукции отсюда получаем верность неравенства для всех остальных степеней двойки, то есть для чисел вида 
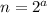при любом натуральном 
. Это утверждение назовём Леммой 1.
Осталось доказать, что из верности неравенства для n=k, следует его верность для n=k-1. Это будет наша Лемма 2.
Ну что же, раз в задании дана такая превосходная подсказка - воспользуемся ей. Найдём такой x, о котором идёт речь в задании. Он выражается из данной в условии формулы очевидным образом, не буду на этом останавливаться:
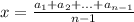
Теперь пусть неравенство верно для произвольного n=k.
Применим это неравенство к числам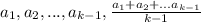 
:
![\frac{a_1+...+a_{k-1}+\frac{a_1+...+a_{k-1}}{k-1} }{k} \geq \sqrt[k]{a_1...a_{k-1}\frac{a_1+...+a_{k-1}}{k-1}}](/tpl/images/1381/5136/dad0f.png)
Что получится в левой части мы знаем - среднее арифметическое чисел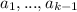 
. Далее возводим неравенство в степень k и преобразовываем:
![\bigg(\frac{a_1+...+a_{k-1}}{k-1} \bigg)^k\geq a_1...a_{k-1}\frac{a_1+...+a_{k-1}}{k-1}\\\bigg(\frac{a_1+...+a_{k-1}}{k-1} \bigg)^{k-1}\geq a_1...a_{k-1}\\\frac{a_1+...+a_{k-1}}{k-1}\geq \sqrt[k-1]{a_1...a_{k-1}}](/tpl/images/1381/5136/97357.png)
Получили как раз неравенство для n=k-1.
Собственно, неравенство можно считать доказанным. Лемма 1 и Лемма 2 решают вопрос для любого n. В самом деле, возьмём произвольное натуральное n. Очевидно, найдётся такое натуральное , что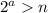 
. Неравенство верно для этой степени двойки (Лемма 1). Но оно верно также и для всех натуральных чисел меньших её, это по индукции следует из Леммы 2. Тогда неравенство верно и для нашего произвольно выбранного n.
1 -3x < (x+2)/3 -(x-1)/2 || *6 || ⇔ 6 - 18x < 2x+4 - 3x+3 ⇔ -1 < 17x ⇔ - 1< 17x ⇔ x > -1/17 , иначе x ∈ ( -1/17 ; ∞)
- - - - - - -
√ -3(k -1/15) ОДЗ: -3(k -1/15) ≥ 0 ⇔ k -1/15) ≤ 0 ⇔ k ≤ 1/15 ,
иначе x ∈ ( - ∞ ;1/17 ]
- - - - - - -
3(x-2) -5 ≥ 2(x-3) ⇔3x- 6 - 5 ≥ 2x - 6 ⇔ 3x -2x ≥ 5 ⇔ x ≥ 5. || x ∈ [5 ; ∞ ) ||
наименьшее целое решение этого неравенства x = 5
- - - - - - -
(x+4)² -x² < 5x +13 ⇔ x²+2*x*4 +4² - x² < 5x + 13⇔8x+16 < 5x + 13 ⇔
8x- 5x < 13 - 16 ⇔ 3x < -3 ⇔ x < -1 иначе x ∈ ( -∞ ;1 )
* * * x ∈ ( -Б ; 1 ) * * *
Скучно ))