1) 12х2+16х=3
12х2-16х-3=0
12х2+2х-18х-3=0
2х(6х+1)-3(6х+1)=0
(6х+1)(2х-3)=0
6х+1=0
2х-3=0
х1=-1/6
х2=2/3
3) 8х2-3=5х
8х2-3-5х=0
8х2+3х-8х-3=0
х(8х+3)-(8х+3)=0
(8х+3)(х-1)=0
8х+3=0
х-1=0
х1=-3/8
х2=1
4) х2=18-3х
х2-18+3х=0
х2+6х-3х-18=0
х(х+6)-3(х+6)=0
(х+6)(х-3)=0
х+6=0
х-3=0
х1=-6
х2=3
Объяснение:
Рассмотрим основные свойства данной функции, которые нам при поиске ответов.
Нули функции, f(x)=0, x²-4x+3=0, x1=1, x2=3.
a=1, ветви параболы направлены вверх.
Минимальное значение f(x) принимает в точке xmin = (x1+x2)/2 = 2.
f(2) = -1.
1. Область определения (-∞; +∞).
2. Область значений [-1; +∞).
3. Минимальное значение f(x) принимает в точке xmin = 2, f(2) = -1.
4. Ось симметрии x=2.
5. Нули функции x1=1, x2=3.
6. f(x)>0, при х∈(-∞;1)∪(3;+∞).
f(x)<0, при х∈(1;3).
7. f(x) убывает при х∈(-∞;2), f(x) возрастает при х∈(2;+∞).
(вроде правильно)
Объяснение:
а). D(y)=R
б). E(y)=R
в). Находим первую производную функции:
y' = 2·x-4
Приравниваем ее к нулю:
2·x-4 = 0
x1 = 2
Вычисляем значения функции
у(2) = -1
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y'' = 2
Вычисляем:
y''(2) = 2>0 - значит точка x = 2 точка минимума функции.
г). Ось симметрии параболы проходит через вершину и перпендикулярно оси Х. Координата х вершины:
х = -b/(2a) = (-4)/2 = -2
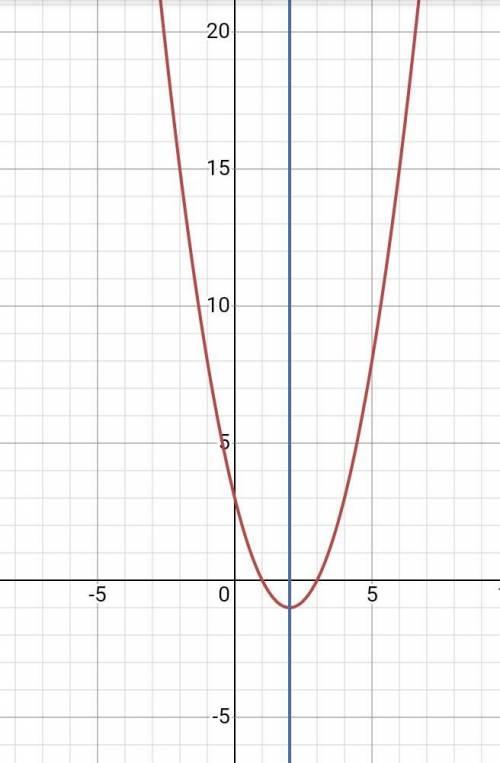
Уравнение оси симметрии: х=2 (смотри график)
д). х²-4х+3=0
х1=1, х2=3
Объяснение: