Задание №2
Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны.
а) 2,3 и 4
Тупоугольный, т.к. против большей стороны лежит больший угол.
б) 6,10 и 11
Тупоугольный, т.к. против большей стороны лежит больший угол.
в) 8,15 и 17
Тупоугольный, т.к. против большей стороны лежит больший угол.
Задание №3
Дан треугольник ABC
AB = 12 см
BC = 10 см
sin A = 0.2
sin C = ?
По теореме синусов
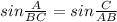
Отсюда 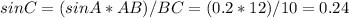
Задание №4
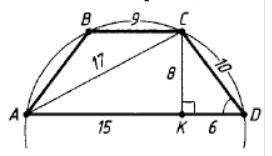
Рисунок приложил.
a) Решение. Из вершины С меньшего основания ВС трапеции АВСD опустим перпендикуляр СК на большее основание AD. Тогда СК = 8. Если AD = 21, ВС = 9 то
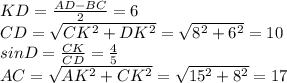
Если R - радиус окружности, описанной около трапеции ABCD , то
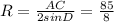
1) ||x - 1| - 1| = 1
Распадается на два уравнения
a) |x - 1| - 1 = -1
|x - 1| = 0; x1 = 1
b) |x - 1| - 1 = 1
|x - 1| = 2
x - 1 = -2; x2 = -1
x - 1 = 2; x3 = 3
ответ: x1 = 1; x2 = -1; x3 = 3
2) ||x - 1| - 1| = 2
Распадается на два уравнения
a) |x - 1| - 1 = -2
|x - 1| = -1
Решений нет
b) |x - 1| - 1 = 2
|x - 1| = 3
x - 1 = -3; x1 = -2
x - 1 = 3; x2 = 4
ответ: x1 = -2; x2 = 4
3) ||x + 2| - 2| = 1
Распадается на два уравнения
a) |x + 2| - 2 = -1
|x + 2| = -1
Решений нет
b) |x + 2| - 2 = 1
|x + 2| = 3
x + 2 = -3; x1 = -5
x + 2 = 3; x2 = 1
4) ||x + 2| - 2| = 2
Распадается на два уравнения
a) |x + 2| - 2 = -2
|x + 2| = 0; x3 = -2
b) |x + 2| - 2 = 2
|x + 2| = 4
x + 2 = -4; x4 = -6
x + 2 = 4; x5 = 2
ответ: x1 = -5; x2 = 1; x3 = -2; x4 = -6; x5 = 2