Нехай за 
год перший робітник виконає завдання, а за 
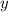год — другий. Тоді за одну годину перший робітник виконає 
усього завдання, а другий робітник — 
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто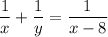 
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто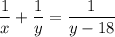 
Складаємо систему з двох рівнянь:
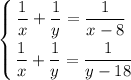
Тут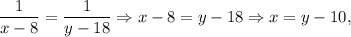 
оскільки ліві частини рівнянь рівні.
Підставимо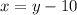 
в перше рівняння:
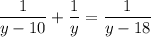
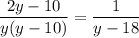
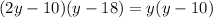
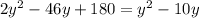
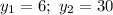
Якщ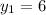о 
, то 
— не відповідає сенсу задачі.
Якщ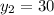о 
, то 
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.
(3p-5)^2-4(3p^2-11p-6)>=0. При таких "p" у исходного уравнения найдутся(возможно, совпадающие) корни x1 и x2. Запишем для них теорему Виета:
x1+x2=-b/a=5-3p
x1*x2=c/a=3p^2-11p-6
Теперь,не вычисляя корней, можно найти сумму их квадратов через "p": x1^2 + x2^2.
Выделим полный квадрат:
(x1+x2)^2-2x1*x2= (5-3p)^2-2(3p^2-11p-6).
По условию, эта сумма квадратов равна 65.
Получаем:
(5-3p)^2-2(3p^2-11p-6)=65
Решим его:
25-30p+9p^2-6p^2+22p+12-65=0
3p^2-8p-28=0
D=(-8)^2-4*3*(-28)=400
p1=(8-20)/6=-2
p2=(8+20)/6=14/3
Проверим, подставив эти значения "p" в исходное уравнения, чтобы убедиться, что дискриминант неотрицателен.
Проверять здесь не буду из-за экономии времени. Все найденные "p" подходят.
Теперь найдем корни уравнения:
1)p=-2
x^2-11x+28=0
x1=4; x2=7
2)p=14/3
x^2+9x+8=0
x1=-8; x2=-1
ответ: при p=-2 x1=4, x2=7; при p=14/3 x1=-8, x2=-1.