ответ:-6,5
Объяснение:
подставляем в уравнение значение х=3, решаем уравнение относительно с
2х^2+7x+c =0
2*9+7*3+c=0 c=-39
теперь имеем 2х^2+7x-39=0
D=49-4*2*(-39)=361=19^2
x1=(-7+19)/4=3
x2=(-7-19)/4=-6,5
Объяснение:
Задание 2.
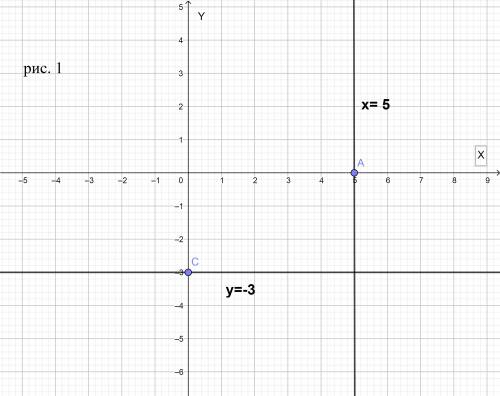
а) Координату х=5 будут иметь все точки , лежащие на прямой , которая параллельна оси ординат и проходит через т.А на оси абсцисс. Любая другая точка координатной плоскости имеет абсциссу отличную от х=5
б) Координату у=-3 будут иметь все точки , лежащие на прямой , которая параллельна оси абсцисс и проходит через т.С на оси ординат. Любая другая точка координатной плоскости имеет ординату отличную от у=-3
рисунок 1 во вложении
Задание 3.
а) На координатной плоскости неравенство х ≥ 4 задаст полуплоскость , которая будет расположена правее прямой х=4. Все точки этой полуплоскости будут иметь абсциссу равную 4 и больше
рисунок 2 во вложении
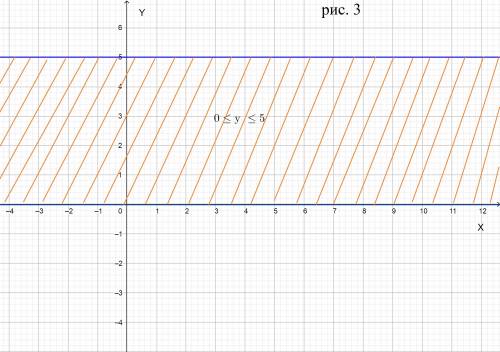
б) Двойное неравенство 0 ≤ у ≤ 5 задает на координатной плоскости две горизонтальные полосы , которые имееют ординату 0 и 5
рисунок 3 во вложении
Задание 4.
а) у = х;
найдем точки и построим график
х=0, у=0
х=3 , у=3
х=-3, у= -3
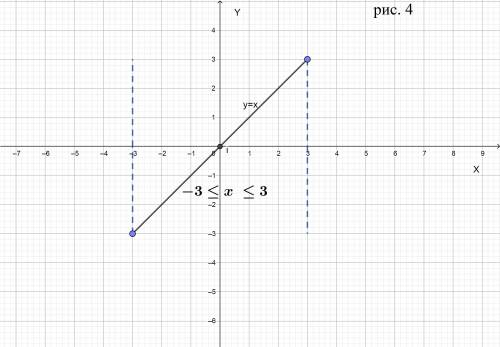
б) –3 ≤ х ≤ 3.
неравенство задает на координатной плоскости две вертикальные полосы, которые имею абсциссу 3 и -3
Изобразим множество точек на координатной плоскости
рисунок 4 во вложении
Задание 5
Решение во вложении
Задание 6
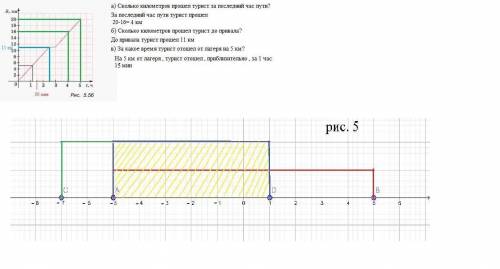
Если | x | ≤ 5 , значит -5 ≤ х ≤ 5, т.е. х ϵ [-5 ; 5]
Отметим этот промежуток т.А и т.В на координатной прямой ( рис. 5 во вложении)
Отметим промежуток –7 ≤ x ≤ 1 , т.е. х ϵ [ -7 ; 1] на координатной прямой т.С и т. D
Для того, чтобы определить границы промежутков [-5; 5] и [-7; 1] сравним левые и правые границы этих промежутков. Поскольку -7 < -5, а 5 >1 , то искомое пересечение имеет вид: х ϵ[-5; 1]

В вопросе опечатка? Может вместо с х?
2х^2+7х+х=0
2х^2+8х=0
2х(х+4)=0
х(х+4)=0
х=0
х+4=0
х=0
х=-4
ответ: х1=-4, х2=0
Если не опечатка и там с, то:
2х^2+7х+с=0
D=7^2-4*2c
D=49-8c
49-8c>0
49-8c=0
49-8c<0
c<49/8
c=49/8
c>49/8
ответ: с<49/8 - два действительных корня; с=49/8 - 1 действительный корень; с>49/8 нет действительных корней.
Или
2х^2+7х+с=0
с=-2х^2-7х
ответ: с=-2х^2-7х, х∈R