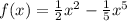
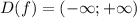 - множество всех действительных чисел.
- множество всех действительных чисел.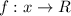 называется четной, если выполняется равенство:
называется четной, если выполняется равенство: 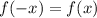 , а нечётной -
, а нечётной - 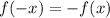
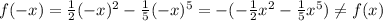
![0,5x^2-0.2x^5=0\\ x^2(0.5-0.2x^3)=0\\ x_1=0;\,\,\,\,x_2= \frac{ \sqrt[3]{20} }{2}](/tpl/images/0410/7783/98bff.png)
![(0;0),\,( \frac{ \sqrt[3]{20} }{2} ;0)](/tpl/images/0410/7783/6ae5e.png) - точки пересечения с осью Ох
- точки пересечения с осью Ох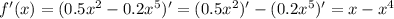
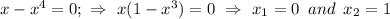
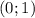 , а убывает на промежутке -
, а убывает на промежутке - 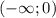 и
и 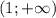 . В точке
. В точке 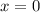 функция имеет локальный минимум, а в точке
функция имеет локальный минимум, а в точке 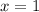 - локальный максимум
- локальный максимум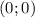 - относительный минимум,
- относительный минимум, 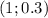 - относительный максимум
- относительный максимум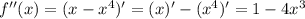
![1-4x^3=0;\,\,\,\Rightarrow\,\,\,x= \frac{ \sqrt[3]{2} }{2}](/tpl/images/0410/7783/8499d.png)
![f(\frac{ \sqrt[3]{2} }{2})=0.1125 \sqrt[3]{4}](/tpl/images/0410/7783/36850.png) - точка перегиба
- точка перегиба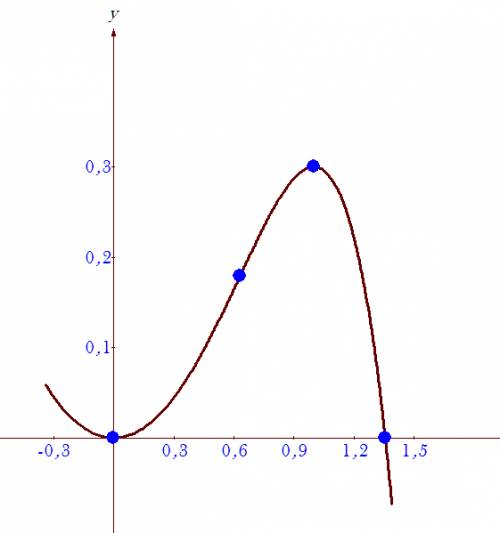
например: если в знаменателе (а-в), то нужно домножить на (а+в)
в данном выражении а=3, в=√(2x-1), тогда (x²-2x)/(3-√(2x-1)) нужно домножить на (3+√(2x+1)), получается
(x²-2x)/(3-√(2x-1))=(x²-2x)(3+√(2x+1))/(3-√(2x-1))(3+√(2x+1))=
(x²-2x)(3+√(2x+1))/(9-2х+1)=(x²-2x)(3+√(2x+1))/(10-2х)
можно также упростить:
х(x-2)(3+√(2x+1))/(10-2х)