Дано: найти площадь между линиями у=sin(x), y=sin(3x) в пределах от х =0 до х = π/2.
Находим точку пересечения линий - это условие sin(x) = sin(3x).
Синус тройного угла равен: sin(3x) = 3sin(x) - 4sin³(x). Подставим:
sin(x) = 3sin(x) - 4sin³(x).
4sin³(x) = 2sin(x).
4sin³(x) - 2sin(x) = 0. Сократим на 2.
2sin³(x) - sin(x) = 0. Вынесем за скобки.
sin(x)(2sin²(x) - 1) = 0. Приравниваем нулю каждый множитель.
sin(x) = 0. х = πк, к ∈ Z.
2sin²(x) - 1, sin(x) = +-1/√2.
x = 2πк +- (π/4), x = 2πк +- (3π/4).
Из этих корней выбираем тот, что находится между 0 и π/2.
Это х = 1/√2 или х = √2/2.
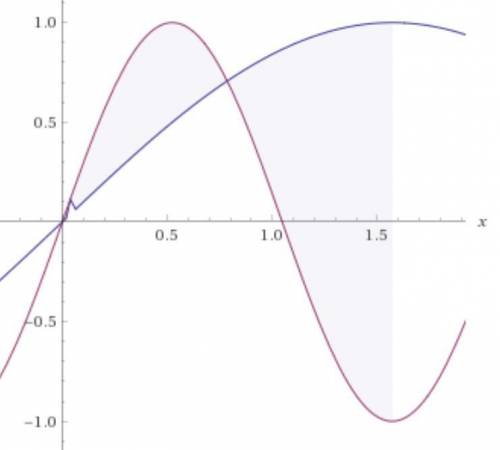
Заданная площадь этой точкой делится на 2 участка.
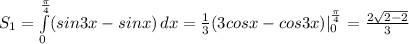 .
.
В числовом выражении S1 ≈ 0,27614.
Аналогично находим:
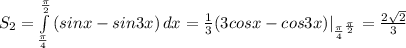
В числовом выражении S2 ≈ 0,94281.
ответ: площадь равна (1/3)*(4√2 - 2) ≈ 1,21895.
-2х^2-11х-5<0 |*(-1)
2х^2+11х+5>0
Решаем как квадратное уравнение:
D=121-40=81
X=-11+-9/4
x1=-5
x2=-1/2
Раскладываем на множители
(х+5)*(х+1/2)>0
Решаем через метод интервалов:
Чертим координатную прямую и выставляем на неё нули уравнения, то есть -5,-1/2:
(-5)(-1/2)>
Точки выколотые, так как знак > строгий и эти точки в ответы не будут
Начинаем определять знаки каждого интервала, начиная с крайнего правого, а именно:
х>-1/2
Берём число больше -1/2, например ноль
И подставляем значение в (х+5)(х+1/2)>0
Вычислять значение необязательно, главное понять какой в итоге знак будет
В первой скобке получается положительный и во второй тоже положительный
++=+, значит интервал положительный
По аналогии делаем с интервалами:
-5<х<-1/2---> получается отрицательным
х<-5---> получается положительным
Теперь координатная прямая выглядит вот так:
(-5)(-1/2)>
+ - +
Нас интересуют значения больше нуля, так как знак >
Значит в ответе будут только да положительных интервала (-~;-5);(-1/2;+~)
Простите за дурацкую координатную прямую
~ это бесконечность, пишется как перевёрнутая восьмёрка, на телефоне просто нет
Надеюсь, всё понятно:)