2. (1б) У якому випадку подію А називають достовірною?
А) р(А)=0Б) р(А) >0 В) р(А)>0,99 Г) р(А)=1
3.(1б) Чому дорівнює медіана сукупності даних 2,2,3,4,5,6,13?
А) 5Б) 4 В) 3Г) 2
4. (1б) Скільки варіантів контрольної роботи з математики можна скласти, маючи 6
задач з алгебри, 5 задач з геометрії, 4 задачі з тригонометрії?
А) 6 Б) 15 В) 120 Г) Інша відповідь
5.(1б) У коробці лежать 12 кольорових олівців, з яких 2 – сині. Яка ймовірність
того, що навмання взятий із коробки олівець буде синім?
А) Б) В) Г)
6. (1,5б) Установіть відповідність між центральною тенденцією вибірки (1-3) та її
значенням (А-Г)
1. Середнє значення вибірки: 12; 17; 11; 13; 14; 15; 15; 16; 13; 13 А. 13
2. Мода вибірки: 12; 17; 11; 13; 14; 15; 15; 16; 13; 13 Б. 13,5
3.Медіана вибірки: 12; 17; 11; 13; 14; 15; 15; 16, 13, 13 В. 13,7
Г. 13,9
7. (2б) У класі 15 хлопців і 12 дівчат. Скількома можна вибрати: а)
хлопця; б) дівчину; в) одного учня цього класу; г) двох учнів — хлопця й дівчину?
8.(2б) В ящику 30 куль: 14 зелених і 16 чорних. З ящика навмання виймають одну
кулю. Визначити ймовірність того що ця куля:
а) зелена, б) чорна, в) біла.
9.(2б)Задано вибірку, яка характеризує місячний прибуток підприємців (у тис грн):
21, 19, 17, 23, 18, 22, 25, 20, 19, 18, 24, 21, 23, 17, 24, 25, 19, 20, 18, 22.Скласти
варіаційний ряд вибірки.Обчислити моду, медіану, середнє значення
вибірки.Побудувати гістограму.
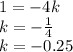
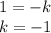
Даны координаты вершин пирамиды:
A(4, 4, -10) ; B(4, 10, 2) ; C(2, 8, 4) ; D(9, 6, 4).
1) уравнение плоскости АВС и ее нормальный вектор
Находим векторы АВ и АС.
АВ = (0;6; 12), АС = (-2; 4; 14).
Их векторное произведение равно.
i j k | i j
0 6 12 | 0 6
-2 4 14 | -2 4 = 84i - 21j +0k - 0j - 4+ 12k = 36i - 24j + 12k.
Нормальный вектор к плоскости АВС равен (36; -24; 12).
Его же можно выразить, разделив на кратную величину 12:
(3; -2; 1).
Уравнение плоскости АВС найдём по точке А и нормальному вектору : A(x − x0) + B(y − y0) + C(z − z0) = 0
Если теперь в уравнении раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:
Ax + By + Cz + D = 0 ,
где D = −Ax0 − By0 − Cz0, A = 3, B = -2, C = 1, точка A(4, 4, -10).
Найдём значение D:
D = -3*4 - (-2)*4 - 1*(-10) = -12 + 8 + 10 = 6.
Уравнение АВС: 3x - 2y + z + 6 = 0.
2) отрезки, которые отрезает плоскость АВС от осей координат.
Для этого уравнение плоскости АВС представить в "отрезках".
Уравнение АВС: 3x - 2y + z + 6 = 0.
3x - 2y + z = -6. Разделим обе части уравнения на -6:
(3/-6)x - (2/-6)y + (1/-6)z = 1.
Получаем: (-1/2)x + (1/3)y + (-1/6)z = 1.
Это и есть длины отрезков, отсекаемые плоскостью АВС на осях:
Ох: (-1/2), Оу: (1/3), Oz: ((-1/6).
3) уравнение плоскости pi, которое проходит через вершину D параллельно к грани ABC.
Общее уравнение заданной плоскости имеет вид:
Ax+By+Cz+D=0 (2)
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (2) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (2). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (2):
Ax0+By0+Cz0+D=0. (3)
Решим (3) относительно D:
D=−(Ax0+By0+Cz0) (4)
Координаты нормального вектора определены:
A = 3, B = −2, C = 1.
Подставляя координаты точки D и координаты нормального вектора в (4), получим:
D=−(Ax0 + By0 + Cz0) = −(3*9 + (−2)*6 +1*4) = −19.
Подставляя значения A, B, C, D в (2), получим уравнение плоскости, проходящей через точку D(9, 6, 4) и параллельной плоскости ABC:
3 x − 2 y + z − 19 = 0.