Объяснение:
во всех случаях выражение под квадратным корнем не должно быть отрицательным, поскольку в таких случаях значений нет:
1)
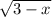
х≠4, и не может быть больше четырёх, уже поскольку 3–4= –1, поэтому х имеет смысл на промежутке (–∞; 3)
2)

х≠2 и х не может быть больше 2, поэтому выражение имеет смысл при х (–∞; 1)
3)
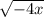
при х (–∞; 0)
4)

при х (3,5; +∞)
5)
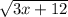
в этом случае х не может быть –5, поскольку 3×(–5)+12= –15+12= –3, поэтому выражение имеет смысл при х (–4; +∞)
6)
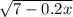
в этом случае х максимум может быть 35, поскольку 35×0,2=7, и выше быть уже не может, поэтому выражение имеет смысл при х (–∞; 35)
1) ищем производную
2) приравниваем её к нулю, решаем получившееся уравнение
3) смотрим: какие корни попали в указанный промежуток
4) вычисляем значения данной функции в этих корнях и на концах промежутка.
5) пишем ответ
начали?
1) y' = 2Сosx + 24/π
2) 2Сosx + 24/π = 0
2Сosx -= - 24/π
Сosx = - 12/π
нет решений
3) решений нет, значит, в функцию подставим концы промежутка и найдём из ответов наибольшее значение.
4) а) х = -5π/6
у = 2Sin(-5π/6) +24*(-5π/6)/π + 6 = -2*1/2 - 20 +6 = -1 -20 +6 = -13
б) х = 0
у = 0+0 +6 = 6
ответ: max y = 0