Для проверки принадлежности точек к линейной функции, нужно подставить значения координат x и y каждой точки в уравнение функции и проверить, выполняется ли равенство.
Давайте проверим каждую точку по порядку:
1. Точка A(0,5;-0,5):
Подставляем координаты x и y:
-0.5 = 5 * 0.5 - 3
-0.5 = 2.5 - 3
-0.5 = -0.5
Равенство выполняется, значит, точка A принадлежит графику функции.
2. Точка B(2;7):
Подставляем координаты x и y:
7 = 5 * 2 - 3
7 = 10 - 3
7 = 7
Равенство выполняется, значит, точка B принадлежит графику функции.
3. Точка C(-0,2;-4):
Подставляем координаты x и y:
-4 = 5 * (-0.2) - 3
-4 = -1 - 3
-4 = -4
Равенство выполняется, значит, точка C принадлежит графику функции.
4. Точка D(-0,5;-6,5):
Подставляем координаты x и y:
-6.5 = 5 * (-0.5) - 3
-6.5 = -2.5 - 3
-6.5 = -5.5
Равенство не выполняется, значит, точка D не принадлежит графику функции.
5. Точка E(1;2):
Подставляем координаты x и y:
2 = 5 * 1 - 3
2 = 5 - 3
2 = 2
Равенство выполняется, значит, точка E принадлежит графику функции.
6. Точка F(1,5;5,5):
Подставляем координаты x и y:
5.5 = 5 * 1.5 - 3
5.5 = 7.5 - 3
5.5 = 4.5
Равенство не выполняется, значит, точка F не принадлежит графику функции.
Итак, точки A, B, C и E принадлежат графику линейной функции y = 5x - 3, а точки D и F не принадлежат.
1){х^2+у^2=25,
{ху=12.
2){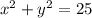
{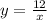
3)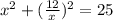
4)x=-3
x=3
x=-4
x=4
5)-3y=12
3y=12
-4y=12
4y=12
6)y=-4
y=4
y=-3
y=3
7)(x1,y1)=(-3,-4)
(x2,y2)=(3,4)
(x3,y3)=(-4,-3)
(x4,y4)=(4,3)
8){(-3)^2+(-4)^2=25
{-3*(-4)=12
{3^2+4^2=25
{3*4=12
{(-4)^2+(-3)^2=25
{-4*(-3)=12
{4^2+3^2=25
{4*3=12
8) {25=25
{12=12
{25=25
{12=12
{25=25
{12=12
{25=25
{12=12
9)(x1,y1)=(-3,-4)
(x2,y2)=(3,4)
(x3,y3)=(-4,-3)
(x4,y4)=(4,3)
Объяснение: