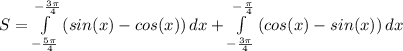 .
.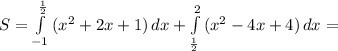
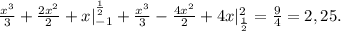
Объяснение:
Решаем графически.
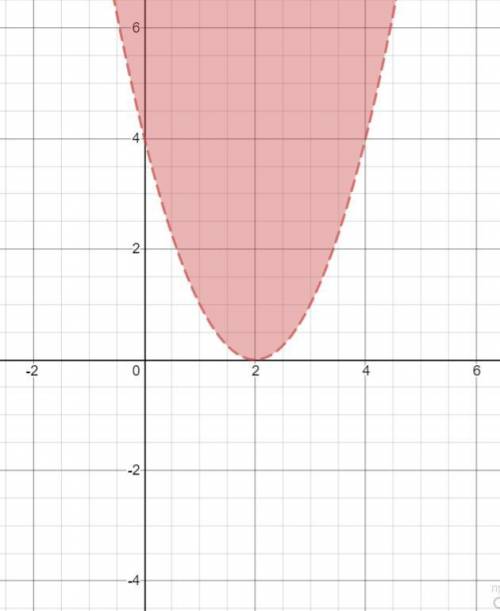
1) Решением первого неравенства является область координатной плоскости над графиком функции

Решение первого неравенства выделено красной областью на первой картинке.
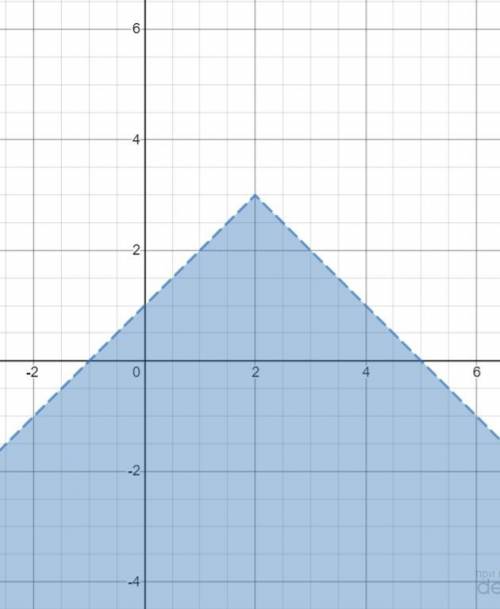
2) Решением второго неравенства является область координатной плоскости под графиком функции
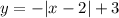
Решение второго неравенства выделено синей областью на второй картинке.
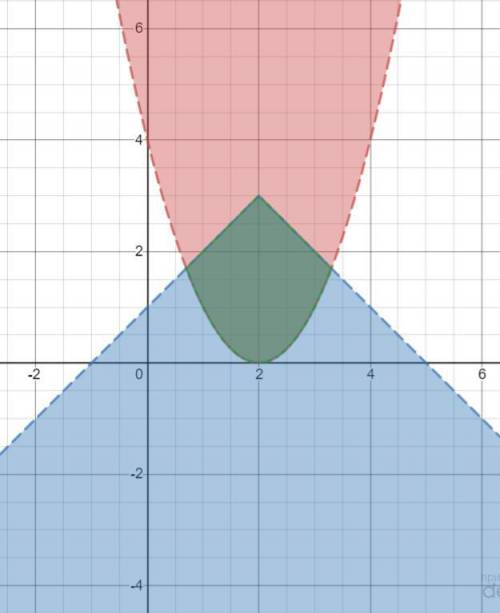
Тогда решением системы неравенств является область, образованная пересечением двух предыдущих областей.
Решение системы выделено зеленой областью на третьей картинке.
Смотря для какого класса - можно двумя Чтобы найти делители составного числа 210, предварительно раскладываем его на простые множители:
210 I 2
105 I 3
35 I 5
7 I 7
1 I , перемножением же простых множителей по два, по три, по четыре и т.д., получаем составные делители данного числа:
2*3=6 3*7=21
2*5=10 2*3*7=42
2*7=14 5*7=35
3*5=15 2*5*7=70
2*3*5=30 3*35=105
1,2,3,5,6,7,10,14,15,21,30,35,42,70,105,210
ответ: 16 делителей
Если для 7-го класса и старше, то можно так:
210=2*3*5*7 = 2^1 * 3^1 * 5^1 * 7^1. т.е. каждый делитель имеет вид:
2^k * 3^l * 5^m * 7^n, где k, l, m,n - целые числа от 0 до 1.
Выбор каждого делителя разбиваем на 4 шага (выбор k, l, m, n), а каждый шаг осуществляем двумя спсобами (0; 1) и тогда получим:
210= 2^1 * 3^1 * 5^1 * 7^1 = 2*2*2*2 = 16
Дтвет: 16 делителей