1) f(x) = x^2 - 6x + 5
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 2x - 6 = 2(x - 3)
f`(x) = 0
2(x - 3) = 0
x = 3
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; 3) і зростає якщо х ∈ (3; +∞)
2) знайдемо точки екстремума.
х(min) = 3 ⇒ y(min) = 3² - 6 * 3 +5 = 9 - 18 + 5 = -4
точки max не існеє.
2) f(x) = x^4 - 2x^2
D(f) = R
1) Знайдемо проміжки монотоності:
f`(x) = 4x³ - 4х = 4х(x² - 1) = 4х(х - 1)(х + 1)
f`(x) = 0
4х(х - 1)(х + 1) = 0
х = 0, х = 1, х = -1
(дивись малюнок)
f(x) спадає якщо х ∈ (-∞; -1) і (0; 1);
зростає якщо х ∈ (-1; 0) і (1; +∞)
2) знайдемо точки екстремума.
х(min) = -1 ⇒ y(min) = (-1)⁴ - 2 * (-1)² = 1 - 2 = -1
х(min) = 1 ⇒ y(min) = 1⁴ - 2 * 1² = 1 - 2 = -1
х(max) = 0 ⇒ y(max) = 0⁴ - 2 * 0² = 0

a) 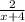
b) 
Объяснение:
Будем раскладывать на множиели при этой формулы :
ax² + bx +c = a(x - x₁)(x - x₂)
a) Для начала нам потребуется найти корни :
x² - x -20 = 0
{ x₁ + x₂ = 1 (система)
{ x₁ × x₂ = -20
x₁ = - 4
x₂ = 5
⇒ x² - x -20 = 1(x - (-4))(x - 5) = (x+4)(x-5)
Теперь подставляем это выражение в знаменатель, а также раскладываем на множители числитель :
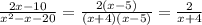
b) Так же, как и в примере, нам нужно найти корни, но уже двух многочленов : (x²+12x+27) и (x²+8x-9).
x² + 12x + 27 = 0
Буду решать через выделение полного квадрата :
(x + 6)² - 9 = 0
(x + 6)² = 9
x+6 = -3 x+6 = 3
x₁ = -9 x₂ = -3
⇒ x² + 12x + 27 = 1(x - (-9))(x - (-3)) = (x+9)(x+3)
Теперь разложим многочлен на множители, который в знаменателе :
x² + 8x - 9 = 0
Решаю опять же через выделение полного квадрата :
(x + 4)² - 25 = 0
(x + 4)² = 25
x+4 = -5 x+4 = 5
x₁ = -9 x₂ = 1
⇒ x² + 8x - 9 = 1(x - (-9))(x - 1) = (x+9)(x-1)
Теперь подставляем эти два выражения :
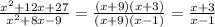
Скорость1 = 90, Скорость2 = 70
Объяснение:
Составляем систему уровнений:
2.5x+2.5y=400
20x-20y=400
Вынесим коэфициенты за скобы:
2.5(x+y)=400
20(x-y)=400
Поделим окончательное значение на коэфициенты и получем:
x+y=160
x-y=20
сложения найдем x:
x+y+x-y=180
2x=180
x=90
И подставим это значение в любое из уровнений, и найдем у:
90-y=20
y=70