^2 - в квадрате
144.
a) s^2
б) 0
в) -6x^2y
г) -4cd
д) 13v^2
e) 62d^3
145.
a) a^2 -3ab+b^2-a^2+3ab+b^2 = 2b^2
б) x^2 +x+1+x^2-x+1 = 2x^2 + 2
в) 4k^2+2k+1-4k^2+2k-1 = 4k
надеюсь что все понятно).
1+sin2x-sinx=cosx
cos^2(x)+sin^2(x)+2sinxcosx-sinx-cosx=0
(sinx+cosx)^2-(sinx+cosx)=0
(sinx+cosx)(sinx+cosx-1)=0
sinx+cosx=0|:cosx не равный 0 или sinx+cosx-1=0
tgx+1=0 sinx+cosx=1
tgx=-1 sqrt{2}cos(П/4-x)=1
x=-П/4+Пn, n принадлежит N cos(П/4-x)=1/sqrt{2}
cos(П/4-x)=sqrt[2}/2
П/4-x=(+-)П/4+2Пn, n N
-x=(+-)П/4-П/4+2Пn, n N
x=(-+)П/4+П/4-2Пn, n N
1) Выносим tgx,получаем:tgx(tgx+1)=0.Каждый множитель приравниваем к нулю:tgx=0 и (tgx+1)=0.Решаем по отдельности: tgx=0 ; x=Пk, где k принадлежит Z.(tgx+1)=0;tgx=-1;x=-arctg1+Gk,где k принадлежит Z.
2)Cosx=кв. корень 3.4;извлекаем корень:Cosx=корень из трех деленое на два;x=+- П/6+2Пk,где k принадлежит Z.
3)Вводим новую переменную: Sinx=t,причем t по модулю меньше равняется 1;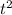 
-4t+3=0,решаем дескрименант,он равен 4,ищем корни: t1=1, t2=4.подставляем сюда Sinx=t,получаем:Sinx=1 x=(-1)в степени n * 1 + Пk,где k принадлежит Z; Sinx=4 по аналогии.
ост. чуть позже.
144.
а) s^2
б) 0
в) -6x^2y
г) -4cd
д) 13v^2
е) 62d^3
145.
а) 2b^2
б) 2x^2 + 2
в) 4k