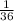tg(α+β) = (tg(α) + tg(β))/(1 - tg(α)·tg(β))
Исходная прямая
y = 2x + 3
её угловой коэффициент
tg(α) = 2
Её надо повернуть на 45°
β = 45°
tg(β) = 1
tg(α+β) = (2 + 1)/(1 - 2·1) = 3/(-1) = -3
Уравнение семейства прямых, угом между которыми и исходной прямой равен + 45°
y = -3x + b
Из этого семейства через начало координат проходит прямая
y = -3x
---
И второе семейство прямых, 45 градусов в отрицательном направлении от исходной
β = -45°
tg(β) = -1
tg(α+β) = (2 - 1)/(1 + 2·1) = 1/3
Уравнение семейства прямых, угол между которыми и исходной прямой равен + 45°
y = x/3 + b
Из этого семейства через начало координат проходит прямая
y = x/3
Решение:
(a-2)/(1+2a)= - 5
Представим левую часть уравнения в виде дроби:
(a-2)/(1+2a)= - 5 / 1
Теперь уравнение представляет собой пропорцию. По основному свойству пропорции произведение её крайних членов ( а это (а - 2) и 1) равно произведению её средних членов ( это ( 1 + 2а) и - 5). Запишем получившееся равенство:
(а - 2) • 1 = (1 + 2а) • (- 5)
Раскроем скобки, выполнив умножение:
а - 2 = - 5 - 10а
Перенесём слагаемые, содержащие переменную, в левую часть уравнения, а не содержащие переменную - в правую часть:
а + 10а = - 5 + 2
Упрощаем:
11а = - 3
Делим обе части уравнения на 11:
а = - 3/11
Проверим, что -3/11 входит в число допустимых значений:
1 + 2а ≠ 0
1 + 2•(-3/11) 1 - 6/11 = 5/11 ≠ 0 - верно.
Запишем ответ:
ответ: - 3/11.
Объяснение:
Карта чёрная: всего в колоде 9 пики, 9 крести, 9 черви и 9 бубен (бубей я не знаю как правильно) 9 пики + 9 черви = 18 чёрных. В итоге получаем: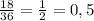
Карта пики: по той же логике всего в колоде 9 пики. Итог: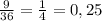
Карта не является числом: всего есть валет, дама, король, туз. И всего 4 масти, получаем, что 4 (валет, дама, король, туз) * 4 (пики, крести, черви и буби) = 16. Итог: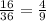
Карта дама: всего 4 дам (пики, крести, черви и буби). Итог: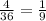
Карта не является девяткой: все карты кроме четырёх девяток (пики, крести, черви и буби). 36 - 4 = 32. Итог: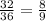
Карта является пиковой девяткой: она всего одна (девятка). Итог: