Объяснение:мы умеем сравнивать дроби с одинаковыми знаменателями и одинаковыми числителями, числители у нас разные, но приводить к общему знаменателю мы умеем.
сравним
2/9 и 5/12, общий знаменатель 36,
2*4/(9*4) и 5*3/(12*3)
8 <15 значит 2/9 < 5/12
сравним
5/12 и 4/15, общий знаменатель 60
5*5/(12*5) и 4*4/(15*4)
25>16
значит 5/12 > 4/15
теперь мы знаем что 5/12 самое большое. надо сравить
2/9 и 4/15 общий знаменатель 45
2*5/(9*5) и 4*3/(15*3)
10 <12
значит 2/9 < 4/15
итого самая маленькая это 2/9 потом 4/15 и 5/12
Другой вариант решения привести все три дроби к одному общему знаменателю.
9=3^2 12=3*2*2 15=3*5, НОК= 2*2*3*3*5=180
2/9=2*20/(9*20)=40/180
5/12=5*15/(12*15)=75/180
4/15=4*12/(15*12)=48/180
в таком виде сравнить дроби просто.
2/9<4/15<5/12
3/8, 5/18 и 10/21
можно применить второй , но тут цифры будут неприятные, так что давайте всё-таки попарно
3/8 5/18
3*9/(8*9) 5*4/(18*4)
27/72 > 20/72
3/8 и 10/21
3*21/(8*21) 10*8/(21*8)
63/168 < 80/168
мы получили что 3/8 меньше 10/21 и больше 5/18, значит последнюю пару сравнивать не нужно можно сразу писать ответ
самое большое это 10/21 потом 3/8 и 5/18
Пояснение:
(!) Одно из свойств уравнений: любое число в уравнении можно перенести через знак равно (т. е. из левой части уравнения в правую, или из правой части в левую. При этом (обычно) переменные переносятся в левую часть уравнения, а числа - в правую) изменив знак перед числом на противоположный ("+" на "-" ; "-" на "+"). Такое уравнение будет равносильно исходному уравнению.
(!) При упрощении выражения и решения уравнения воспользуемся распределительным свойством умножении, относительно действия сложения и вычитания:
a × (b + c) = ab + ac.
a × (b - c) = ab - ac.
1) x (x - 8) - 20 = - 15 - x (1 - x);
x² - 8x - 20 = - 15 - x + x²;
x² - x² - 8x + x = - 15 + 20;
- 7x = 5;
x = 5 ÷ (- 7);
x = - .
.
__________
ответ: - .
.
2) 47 - x (11 - x) = 19x + x²;
47 - 11x + x² = 19x + x²;
x² - x² - 11x - 19x = - 47;
- 30x = - 47;
x = - 47 ÷ (- 30);
x =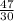 ;
;
x =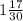
__________
ответ: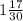 .
.
3) 33x - x² = (35 - x) x - 17;
33x - x² = 35x - x² - 17;
- x² + x² + 33x - 35x = - 17;
- 2x = - 17;
x = - 17 ÷ (- 2);
x = 8,5.
__________
ответ: 8,5.
4) 59x + 4x² = - 4x (1 - x) + 21
59x + 4x² = - 4x + 4x² + 21
4x² - 4x² + 59x + 4x = 21
63x = 21
x = 21 ÷ 63
x =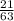
x =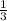 .
.
__________
ответ: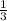 .
.
__________________
Удачи! :)