Из полного комплекта домино случайным образом выбрали одну кость.найдите вероятность того , что на ней числа: 1) 6 и 5 2) 0 и 1 3) одинаковые 4) разные
X²(-x² - 49) ≤ 49(-x² - 49) x²(-x² - 49) - 49(-x² - 49) ≤ 0 // перенесли все слагаемые влево (x² - 49)(-x² - 49) ≤ 0 // вынесли за скобку общий множитель (увидели, что и в x²(-x² - 49), и в 49(-x² - 49) есть (-x² - 49) -(x² - 49)(x² + 49) ≤ 0 // вынесли минус из (-x² - 49) (x² - 49)(x² + 49) ≥ 0 // разделили обе части неравенства на -1, поэтому поменялся знак x² + 49 всегда принимает положительные значения: оба слагаемые положительные, поэтому отрицательное или нулевое значение не получится. Тогда нужно, чтобы x² - 49 был неотрицательным (т.е. положительным + может быть нулем), т.к. иначе все выражение станет отрицательным. x² - 49 ≥ 0 Здесь решайте, как вам нравится: методом интервалов или рисуя параболу. В любом случае, находим нули: это -7; 7 – и наносим их на координатную ось. Если рисуете параболу: графиком функции y = x² - 49 является парабола ветвями вверх (a = 1 > 0), делаете эскиз (то есть рисуете параболу ветвями вверх, проходящую через найденные нули) и расставляете знаки: где парабола принимает отрицательные значения, т.е. располагается ниже оси x, там минус, где выше – там плюс. Нам нужны положительные решения, поэтому мы выбираем, где плюс (ответ чуть ниже). Если решаете методом интервалов: рисуете промежутки: до -7, от -7 до 7 и от 7 – и расставляете на них знаки. Коэффициент перед x > 0, начинаем с знака + (справа налево) и чередуем. ответ ниже. x ∈ (-∞; -7] ∪ [7; +∞).
ответ: x ∈ (-∞; -7] ∪ [7; +∞). Спрашивайте в комментариях, если что-то непонятно.
Найдем уравнение касательной, проходящей через точку с абсциссой
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой
:
Найдем значение производной данной функции в точке с абсциссой
:
Уравнение касательной имеет вид:
Подставим значение
Итак, уравнение касательной заданной функции: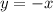
Воспользуемся геометрическим смыслом касательной: коэффициент наклона
касательной 
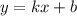численно равен тангенсу угла наклона 
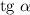с положительным направлением оси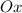 
В найденной касательной коэффициент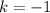
, следовательно, 
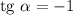при 
или 
ответ:
или 