Найти К, если известно, что график функции y=kx-5 проходит через точку M(-1;4)

👇

Увидеть ответ

Ответ:

milanakpoplove

09.06.2023

Объяснение:

4 = k*(-1) -5

4 = -k -5

k = -5-4

k = -9

4,8(73 оценок)

Открыть все ответы

Ответ:

9872105

09.06.2023

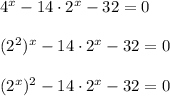
$4^x - 14\cdot 2^x - 32 = 0\\\\(2^2)^x - 14\cdot 2^x - 32 = 0\\\\(2^x)^2 - 14\cdot 2^x - 32 = 0$

Введём замену: 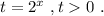$t = 2^x\ , t0\ .$

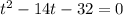
t^2 - 14t - 32 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -32\\t_{1} + t_{2} = 14\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 16; t = -2}$ .

Но так как 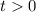t 0 , то -2 не является решением этого уравнения. Выполняем обратную замену:

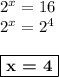
$2^x = 16\\2^x = 2^4\\\\\boxed{\textbf{x = 4}}$

ответ: 4.

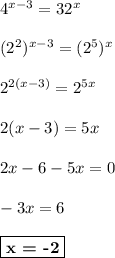
$4^{x-3} = 32^x\\\\(2^2)^{x-3} = (2^5)^x\\\\2^{2(x-3)} = 2^{5x}\\\\2(x-3) = 5x\\\\2x - 6 - 5x = 0\\\\-3x = 6\\\\\boxed{\textbf{x = -2}}$

ответ: -2.

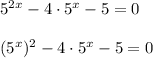
$5^{2x} - 4\cdot 5^x - 5 = 0\\\\(5^x)^2 - 4\cdot 5^x - 5 = 0$

Введём замену: 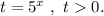$t = 5^x\ ,\ t 0.$

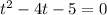
t^2 - 4t - 5 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -5\\t_{1}+t_{2} = 4\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 5; t = -1}$

Но так как 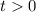t 0 , то -1 не является решением этого уравнения. Выполняем обратную замену:

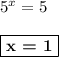
$5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

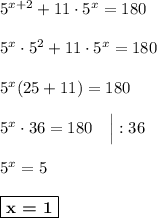
$5^{x+2} + 11\cdot 5^x = 180\\\\5^x \cdot 5^2 + 11\cdot 5^x = 180\\\\5^x(25+11) = 180\\\\5^x\cdot 36 = 180\ \ \ \Big| :36\\\\5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

$9^{\sqrt{x-5}} - 27 = 6\cdot 3^{\sqrt{x-5}}$

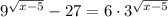
Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:

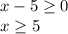
$x - 5 \geq 0\\x \geq 5$

Продолжаем решение:

$(3^2)^{\sqrt{x-5}} - 6\cdot 3^{\sqrt{x-5}} - 27 = 0\\\\(3^{\sqrt{x-5}})^2 - 6\cdot 3^{\sqrt{x-5}} - 27 = 0$

Введём замену: 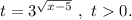$t = 3^{\sqrt{x-5}}\ ,\ t0.$

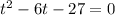
t^2 - 6t - 27 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -27\\t_{1}+t_{2} = 6\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 9; t = -3}$

Но так как 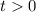t 0 , то -3 не является решением этого уравнения. Выполняем обратную замену:

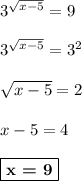
$3^{\sqrt{x-5}} = 9\\\\3^{\sqrt{x-5}} = 3^2\\\\\sqrt{x-5} = 2\\\\x - 5 = 4\\\\\boxed{\textbf{x = 9}}$

ответ: 9.

4,5(82 оценок)

Ответ:

ser73

09.06.2023

а) x² + 4x + 10 ≥ 0

D = 4² - 4· 10 = - 24

График функции у = x² + 4x + 10 - парабола веточками вверх, пересечения с осью Ох нет, т.к. D < 0, поэтому у > 0 и ответ

2) Решением неравенства является вся числовая прямая

b) -x² + 10x - 25 > 0

-(х - 5)² > 0

Поскольку -(х - 5)² < 0 при любых х, то ответ

1) Неравенство не имеет решений

c) x² + 3x + 2 ≤ 0

D = 3² - 4 · 2 = 1

x₁ = 0.5(-3 - 1) = -2

x₂ = 0.5(-3 + 1) = -1

График функции у = x² + 3x + 2 - парабола веточками вверх, пересекает ось Ох в точках с координатами x₁ = -2 и x₂ = -1 поэтому решением неравенства является интервал [-2; -1] , и ответ

4) Решением неравенства является закрытый промежуток.

d) -x² + 4 < 0

x² - 4 > 0

График функции у = x² - 4 - парабола веточками вверх, пересекает ось Ох в точках с координатами x₁ = -2 и x₂ = 2 поэтому решением неравенства является интервалы (-∞; -2) и (2; +∞) , и ответ

6) Решением неравенства является объединение двух промежутков.

4,6(100 оценок)

Это интересно:

Стиль-и-уход-за-собой

26.11.2020

Как сделать боб каре как у Пэрис Хилтон...

Взаимоотношения

29.12.2020

Как игнорировать своего парня: 5 советов для девушек, которые хотят сохранить свою независимость...

Хобби-и-рукоделие

01.02.2020

Как пользоваться моноподом: полезные советы и рекомендации...