ответ:Раскроем скобки:
Тогда наша задача сводится к тому, чтобы доказать, что (n-1)(n+1) при любом нечетном n кратно 8.
Любое нечётное число можно представить в виде: n = 2k+1, k∈Z (Z - множество целых чисел)
Теперь задача сводится к тому, чтобы доказать, что k(k+1) при любом целом k кратно 2.
Пусть k = 0, тогда произведение равно 0 и отсюда следует, что произведение кратно 2;
Пусть k - нечётное число, тогда k+1 - чётное. Произведение не чётного числа на чётное будет чётным и, следовательно, кратным 2.
Аналогично если k - чётное число.
На основании вышеизложенного приходим к выводу, что (4n+1)² – (n+4)² при любом нечётном n кратно 120.
Объяснение:
Пусть Иванов получает за месяц
рублей.
Тогда Петров получает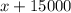
рублей.
И известно, что для того, чтобы купить машину первый из них работал 20 месяцев (и заработал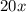
рублей). А второй работал 8 месяцев (заработал: 
). И при этом оба смогут купить одну и ту же машину, то есть количество полученных ими денег одинаковое. Поэтому мы можем составить и решить уравнение:
Получается, что Иванов получает за месяц 10000 рублей. Тогда Петров получает 25000. И машина стоит:
10000 * 20 = 200000 (рублей)
Задача решена!