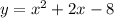
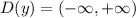
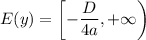 - где D дискриминант.
- где D дискриминант.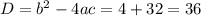
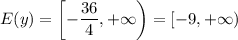
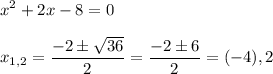



![(-\infty,-1]](/tpl/images/0467/5865/91666.png)
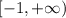

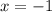
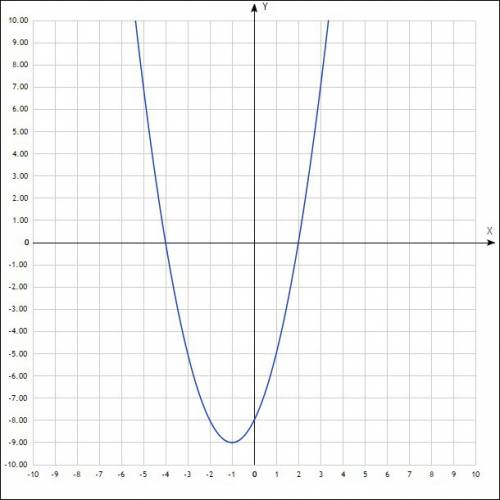
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)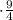 - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: 
9t = 1

Значит, 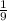 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда 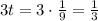 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно, 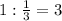 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.

х₁=168/16=10,5
х₂=156/16=9,75
Объяснение:
Решить квадратное уравнение
2(2x−18)²−9(2x−18)+9=0
[2(2x−18)²−9(2x−18)]+9=0
(2x−18)[2(2x−18)-9]+9=0 разложение на множители
[(2x−18)(4x-36-9)]+9=0
[(2x−18)(4x-45)]+9=0
(8x²−90x-72x+810)+9=0
8x²−162x+819=0
х₁,₂=(162±√26244-26208)/16
х₁,₂=(162±√36)/16
х₁,₂=(162±6)/16
х₁=168/16=10,5
х₂=156/16=9,75
Рациональнее использовать разложение на множители