Если к числу Х прибавить 8 и отнять 6, то получим 8. Найти Х Некое число в квадрате - 169. Найти это число К Х прибавили 110 получили 115. Найти Х К Х прибавили 116 получили 115. Найти Х К Х прибавили 110 и отняли 118 получили 117. Найти Х К Х прибавили 1168 получили 115. Найти Х К Х прибавили 110 и умножили на 9. получили 18. Найти Х От Х отняли 6 и прибавили 8. Получили 132. Найти Х От Х отняли 6 и прибавили 8, разделили на 2 Получили 132. Найти Х От Х отняли 15 и прибавили 8. Потом умножили на 7. Получили 49 . Найти Х От Х отняли 6 и прибавили 9. Получили 139. Найти Х От Х отняли 6 и умножали на 8. Получили 32. Найти Х Х разделили на 7 и умножили на 8. Получилось 16. Найти Х Х разделили на 9 и умножили на 4. Получилось 16. Найти Х Х разделили на 7 и умножили на 100. Получилось 16. Найти Х Х разделили на 14 и умножили на 78 Получилось 156. Найти Х Х разделили на 7 и умножили на 8. Получилось 32. Найти Х
1. Подкоренное выражение неотрицательно, знаменатель не равен 0
обьединяя![D(y)=(-\infty;-5) \cup (-5;8]](/tpl/images/0033/6568/ccdfe.png)
2. Область определения - множество всех действительных чисел, x є R
по определению функция g(x) нечетная
3.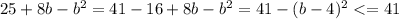 , причем равенство достигается при b=4
, причем равенство достигается при b=4
(так как квадрат любого выражения неотрицателен)
4. График во вложении
при x>=0 график имеет вид y=x^2-8x+13 вершина параболы (4;-3)
при x<0 график имеет вид y=x^2+8x+13 вершина параболы (-4;-3)
5. 2х-1=0
х=0.5 - вертикальная асимптота
ищем наклонные асимптоты
значит наклонная будет одновременно горизонтальной асимптотой и равна y=-3
6. График во вложении
Область определения D(y)=R
Область значений функций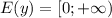
Функция четная, непериодичная
Функция положительная на R/{-2;2}
Нули функции х1=-2, х2=2
Функция убывает на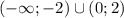
Функция возростает на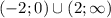
х=-2 и х=2 - точки локального минимума (y(-2)=y(2)=0)
x=0 - точка локального максимума (y(0)=4)
Асимптот функция не имеет