<> Здравствуйте, Xonkil! <>
• ответ:
y = cos(3χ) + cos(3χ)
y = 4cos(2χ)
• Пошаговое Объяснение:
|
| • Корень (n/6+kn/3, 0), k ∈ ℤ
|
| • Область определения x ∈ ℝ
|
| • Минимум (n/3+2kn/3, -2), k ∈ ℤ
|
| • Максимум (2kn/3, 2), k ∈ ℤ
|
| • Пересечение с осью ординат (0,2)
– – – – –
|
| • Корень (n/4+kn/2, 0), k ∈ ℤ
|
| • Область определения х ∈ ℝ
|
| • Минимум (n/2+kn, -4), k ∈ ℤ
|
| • Максимум (kn, 4), k ∈ ℤ
|
| • Пересечение с осью ординат (0, 4)
[ P. s. Ниже указана схема к данной задаче. Если что, она принадлежит мне и чертила я её в специальном приложении. ]
<> С уважением решить! Буду благодарна за не слишком краткий ответ(те чтобы было понятно откуда идёт след">
Без взятия производных для определения наибольшего и наименьшего значений функции приходится строить график этой функции.
График функции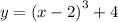 
можно получить из графика 
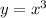следующим образом:
1. График 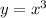сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
2. Полученный график y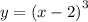
сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
Полученный график функции 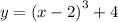показан самым жирным и самым синим на рисунке.
Из графика видим, что на отрезке ![\left[0;3\right]](/tpl/images/0129/5065/c1b3c.png)
рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
Итак, ответ.
![min|_{\left[0;3\right]} y(x) = y(0) = \left(0 - 2\right)^3 + 4 = -8 + 4 = -4](/tpl/images/0129/5065/af09b.png)
![max|_{\left[0;3\right]} y(x) = y(3) = \left(3 - 2\right)^3 + 4 = 1 + 4 = 5](/tpl/images/0129/5065/8238e.png)
x1= 2, x2= -3, x3= 1, x4= -2
Объяснение:
пусть x²+x-3=t, тогда
t/2-3/2t=1
t²-3-2t=0
t²-2t-3=0
D= 4+12= 16
t1= (2+4)/2= 3
t2= (2-4)/2= -1
1) x²+x-3=3
x²+x-6=0
D= 1+24=25
x1= (-1+5)/2= 2
x2= (-1-5)/2= -3
2) x²+x-3=-1
x²+x-2=0
D= 1+8=9
x3= (-1+3)/2= 1
x4= (-1-3)/2= -2