В решении.
Объяснение:
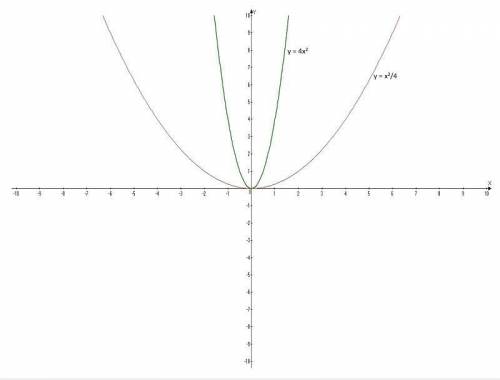
Постройте на одной координатной плоскости графики функций:
1) у = 4х²; у = х²/4;
Графики - параболы с вершиной в начале координат (0; 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = 4х²;
Таблица:
х -2 -1 0 1 2
у 16 4 0 4 16
у = х²/4;
Таблица:
х -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
у 9 6,25 4 2,25 1 0,25 0 0,25 1 2,25 4 6,25 9
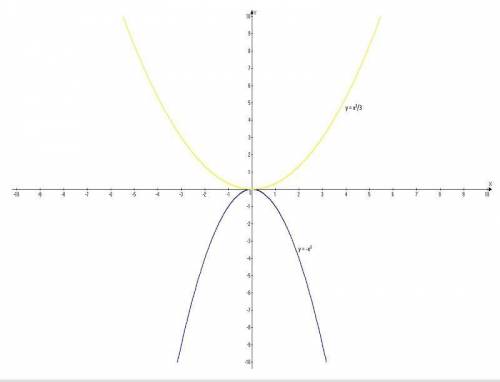
2) у = -х²; у = х²/3;
Графики - параболы с вершиной в начале координат (0; 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -х²;
Таблица:
х -3 -2 -1 0 1 2 3
у -9 -4 -1 0 -1 -4 -9
у = х²/3;
Таблица:
х -6 -3 0 3 6
у 12 3 0 3 12
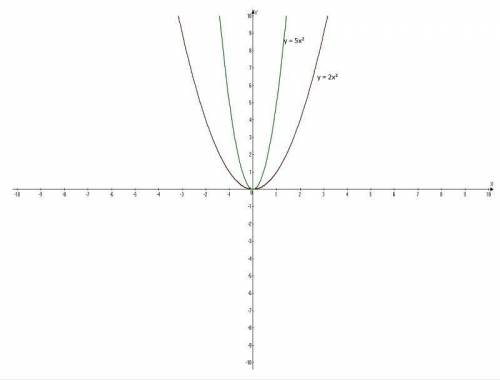
3) у = 2х²; у = 5х²;
Графики - параболы с вершиной в начале координат (0; 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = 2х²;
Таблица:
х -3 -2 -1 0 1 2 3
у 18 8 2 0 2 8 18
у = 5х²;
Таблица:
х -2 -1 0 1 2
у 20 5 0 5 20
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов - ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой "30 градусов", на их пересечении считываем результат - одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других "популярных" углов.
Объяснение:
Arcsin(ctg(π/4))=arcsin(1)=π/ 2 cos(arcsin(-1/2)-arcsin(1))=cos(2π/3-π/2)= cos(4π/6-3π/6)=cos(π/6)=√3/2.