Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²= 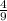
ответ: 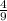
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a= 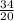
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
совокупность:
3с=5
3с=–5
совокупность:
с= 
с= 
совокупность:
с= 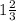
с= 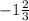
Каждой точке (х; у) графика у = f(x) соответствует единственная точка (х; - у) графика у =- f(x) и наоборот. Точки (х; у) и (х; - у) симметричны относительно оси ОХ. Значит, графики у =f(x) и y = -f(x) симметричны относительно оси ОХ.
Пример 1
Построить график функции у = - .
Решение
Строим график функции у = , а затем строим симметрично относительно оси ОХ.
Симметрия относительно оси ОУ (оси ординат)
Каждой точке (х; у) графика у = f(x) соответствует единственная точка (-х; у) графика у = f(-x), и наоборот. Но точки (х; у) и (-х; у) симметричны относительно оси ОУ, значит, графики у = f(x) и у = f(-x) симметричны относительно оси ОУ.
Пример 2
Построить график функции у = .
Решение
Строим график функции у =, а затем строим симметрично относительно оси ОУ.
Пример 3
Построить график функции у = -
Решение
Выполним ряд последовательных преобразований:
строим график функции у = ;
строим симметрично относительно оси ОУ, т. е. получаем график функции у = ;
строим симметрично относительно оси ОХ, т.е. получаем искомый график функции у = -.
Параллельный перенос (сдвиг) вдоль оси абсцисс
Пусть дан график функции у = f(x).
Чтобы построить график функции у = f(x+a), где а – некоторое данное число, достаточно график функции у= f(x) перенести параллельно направлении оси ОХ на расстояние в положительном направлении, если а<0, и в отрицательном направлении, если а>0.
Пример 4.
Построить графики функций у =(х - 3)² и у =(х + 1)².
Решение
Строим график функции у = х² (пунктиром). Переносим его дважды: в положительном направлении оси ОХ на расстояние, равное 3, и получаем график у = (х – 3)²; в отрицательном направлении оси ОХ на расстояние, равное 1, и получаем график у = (х + 1)².
Параллельный перенос (сдвиг) вдоль оси ординат
Пусть дан график функции у =f(x).
Чтобы построить график функции у = f(x) + a, где а – некоторое данное число, достаточно график функции у = f(x) перенести параллельно оси ОУ на расстояние в положительном направлении, если а >0, и в отрицательном, если а /I>0.
Пример 5.
Построить график функции у = 5+.
Решение
Строим график у = (пунктиром). Переносим его в положительном направлении оси ОХ на расстояние, равное 4, и получаем график у =, а затем переносим в положительном направлении оси ОУ на расстояние, равное 5, получаем искомый график у = 5 +.