а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
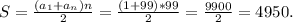
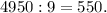
Так как получилось разделить нацело, то 1234...9899 делится на 9.
Расстояние, которое должен проплыть второй второй пловец, до того момента, как он догонит первого пловца обозначим через S. Тогда второй пловец проплывёт S - 70м. Плыть они будут одно и то же время. Значит:
S/80 = (S - 70)/45;
45S = 80S - 5600;
S = 160м;
t = 160/80 = 2 мин.
Аналогично для скорости 52м/сек:
S/520 = (S - 70)/45;
45S = 52S - 3640;
S = 520м;
t = 520/52 = 10 мин, т.е. сможет догнать.
А вот сможет ли второй пловец догнать первого, если он будет плыть с такой же скоростью, как и первый - это навряд ли, это и так понятно.
2)=cos 20°