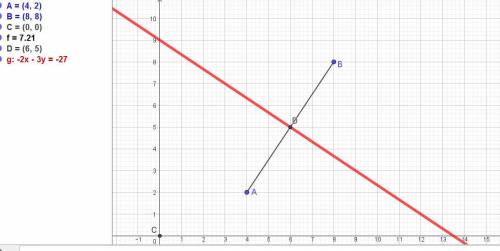
Прямая,все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это перпендикуляр к середине отрезка АВ.
Уравнение АВ: (х - 4)/(8 - 4) =(у - 2)/(8 - 2).
(х - 4)/4 =(у - 2)/6) или (х - 4)/2 =(у - 2)/3.
Или в общем виде Ах + Ву + С = 0.
3х - 12 = 2у - 8,
3х - 2у - 4 = 0. Здесь А = 3, В = -2.
Перпендикулярная прямая имеет вид -Вх + Ау + С1 = 0.
Для определения коэффициента С1 надо подставить координаты точки, принадлежащей этой прямой.
Такая точка - середина АВ (точка Д).
Д = (1/2)(A(4;2) + B(8;8))/2 = (6; 5). Подставляем:
2*6 + 3*5 + С1 = 0,
С1 = -12 - 15 = -27.
ответ: уравнение прямой, все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это 2х + 3у - 27 = 0.
научиться выделять общие множители и приводить подобные члены
находить общий знаменатель и выполнять действия с дробями
переписывание чужих решений пользы не приносит, от слова совсем
условия вы записали не очень понятно, нужно использовать скобки
1) (x^2-9)/2x^2 +36x/9x^2 - 6x + x^2 = (9x^2 - 81 +72x -108x^3 +18x^4)/18x^2=
=(18x^4 -108x^3 +9x^2 +72x -81)/18x^2 = (2x^4 -12x^3 +x^2 +8x -9)/2x^2
2) (2a +x +2a -x)/(4a^2 - x^2)
3) a +a - ab/b = (ab +ab -ab)/b = ab/b если сократить то =a
4) (2b -3ax)/ 6x^2 что-то напутали наверное в условии