Непустое подмножество линейного пространства называется линейным подпространством, если линейные операции, то есть сложение векторов и умножение их на число, не выводят за пределы этого множества. Аксиомы линейного пространства для этого множества проверять не обязательно - они будут выполнены автоматически.
1) Умножив такой вектор на отрицательное число, получим вектор, конец которого лежит во второй четверти. Поэтому ответ в первом случае отрицательный.
2) Складывая векторы, у которых координаты с четными номерами равны 0, а также умножая такие векторы на любое число, снова получаем вектор из этого множества. Поскольку оно непусто, оно является линейным подпространством.
3) Складывая векторы, у которых координаты с четными номерами равны между собой, а также умножая такие векторы на любое число, снова получаем вектор из этого множества. Поскольку оно непусто, оно является линейным подпространством.
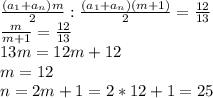
12 не знаю, там корень 88 выходит в дискриминанте
прикрепила на фото графики
13) 3y^2+7y+4<0
D=b^2-4ac=49-4*3*4=49-48=1
x1=-b-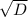
/2a=-7-1/6=-4/3=-1 1/3
x2=-b+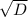
=-7+1/6=-6/6=-1
7) 5x^2-x+6<0
D=b^2-4ac=1-5*6=1-30=-29-нет кореней
6)x^2-7x+6>0
D=49-4*6=25
x1=7-5/2=2/2=1
x2=7+5/2=12/2=6
8)-7x^2+12x+4>0
D=144-4*4*(-7)=144+112=256
x1=-12+16/-14=-4/-14=2/7
x2=-12-16/-14=2