1) Пусть cos x > 0, тогда |cos x| = cos x
sin x > √3*cos x - √2
Делим всё на 2.
1/2*sin x > √3/2*cos x - √2/2
√2/2 > √3/2*cos x - 1/2*sin x
√2/2 > cos x*cos(pi/6) - sin x*sin(pi/6)
cos (x + pi/6) < √2/2
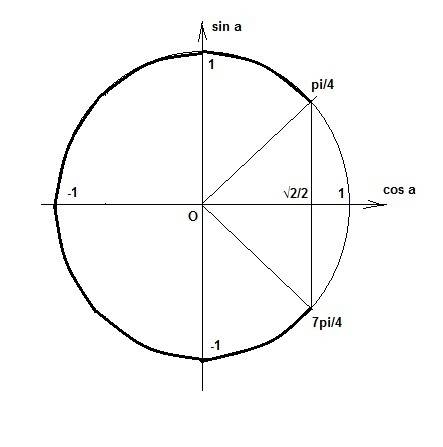
pi/4 + 2pi*k < x + pi/6 < 7pi/4 + 2pi*k
На 1 рис. показано, почему это так.
Интересующая нас часть круга выделена жирной линией.
pi/4 - pi/6 + 2pi*k < x < 7pi/4 - pi/6 + 2pi*k
3pi/12 - 2pi/12 + 2pi*k < x < 21pi/12 - 2pi/12 + 2pi*k
x ∈ (pi/12 + 2pi*k; 19pi/12 + 2pi*k)
С учетом условия cos x >= 0 получаем:
x ∈ (pi/12 + 2pi*k; pi/2 + 2pi*k] U [3pi/2 + 2pi*k; 19pi/12 + 2pi*k)
2) Пусть cos x < 0, тогда |cos x| = -cos x
sin x > -√3*cos x - √2
Делим всё на 2.
1/2*sin x > -√3/2*cos x - √2/2
√3/2*cos x + 1/2*sin x > -√2/2
cos x*cos(pi/6) + sin x*sin(pi/6) > -√2/2
cos (x - pi/6) > -√2/2
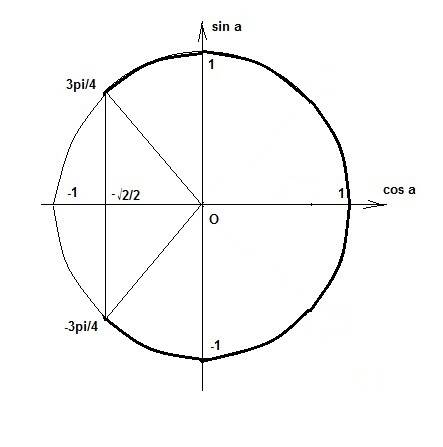
-3pi/4 + 2pi*k < x - pi/6 < 3pi/4 + 2pi*k
На 2 рис. показано, почему это так.
-3pi/4 + pi/6 + 2pi*k < x < 3pi/4 + pi/6 + 2pi*k
-9pi/12 + 2pi/12 + 2pi*k < x < 9pi/12 + 2pi/12 + 2pi*k
x ∈ (-7pi/12 + 2pi*k; 11pi/12 + 2pi*k)
С учетом условия cos x < 0
x ∈ (-7pi/12 + 2pi*k; -pi/2 + 2pi*k) U (pi/2 + 2pi*k; 11pi/12 + 2pi*k)
Если свести оба случая в один ответ, то получится:
x € (-7pi/12 + 2pi*k; -5pi/12 + 2pi*k) U (pi/12 + 2pi*k; 11pi/12 + 2pi*k)
Дана функция у=5х⁴ - 3х² - 1.
y' = 20x³ - 12x.
20x³ - 12x = 4x(5x² -3) = 0.
Получили 3 критические точки: х = 0, х = √(3/5) и х = -√(3/5).
Находим знаки производной на промежутках:
-√(3/5) √(3/5)
x = -1 -0,7746 -0,5 0 0,5 0,7746 1
y' = -8 0 3,5 0 -3,5 0 8 .
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
ответ: имеем один локальный максимум в точке х = 0, у = -1.