y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.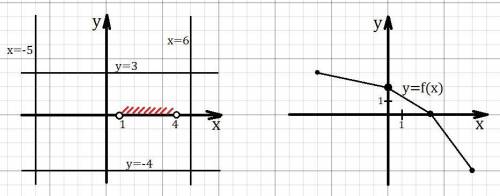
Объяснение:
Решение.
Разберем последовательно как можно просто и без ошибок построить график любой функции.
Для этого первым делом рассмотрим функцию, график которой нужно построить.
Данная функция представлена в виде дроби целого известного числа и неизвестного, причем неизвестное стоит в знаменателе дроби. Вспоминаем математику начальных классов, когда учили, что делить нельзя только на ноль. Из этого делаем вывод, что неизвестное число х для заданной функции может быть каким угодно, кроме нуля. Теперь можно записать область значений переменной х:
Проверим, является ли функция четной. Для этого подставим —х в ее уравнение вместо х и сделаем вывод:
Получаем нечетную функцию. Для нас такая информация полезна тем, что график нечетной функции симметричен началу координат, то есть точке (0; 0).
Найдем точки, которые принадлежат графику, чтобы провести через них кривую. Выберем точки произвольно и подставим вместо х: