Сын мог бы выполнить один всю работу за 60 дней, а отец за 15 дней
Объяснение:
Весь объём работы принимаем за 1 (единицу)
Пусть сын один может выполнить всю работу за х дней, а отец за у дней. Планировалось, что работая вместе, отец и сын смогут выполнить всю работу за 12 дней, значит, за 1 день они сделают 1/12 работы. Составим первое уравнение:
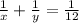
Сын работал 8 дней и за 8 дней сделал 8/х часть работы. Отец работал 8+5 =13 дней и за 13 дней сделал 13/у часть работы. Фактически вместе они выполнили весь объём работы = 1. Составляем второе уравнение:
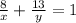
Решаем систему уравнений:

Итак,сын мог бы выполнить один всю работу за 60 дней, а отец за 15 дней.
1. поработаем со знаменателем первой дроби. это формула сокращенного умножения. (х+2)(х-2)- будет являться общим знаменателем.
2. 3 переносим в левую часть, поменяв знак на противоложный, тк переносим через =. подгоним все под общий знаменатель и получим:
4-(х+2)-3(х²-4)\(х-2)(х+2)=0
3. дробь равна 0, когда числитель равен 0, а знаменатель не равен. потому знаменатель отбрасываем. НО. делить на 0 нельзя, поэтому нельзя, чтобы в знаменателе получился 0. х не равно +-2. получим:
4-(х+2)-3(х²-4)=0
4. раскроем скобки. если перед скобкой стоит -, то все знаки меняются на противоположные, а скобки убираются. если перед скобкой стоит умножение, то нужно член, стоящий перед скобкой, умножить на каждый член в скобки и скобки уберутся. получим
4-х-2-3х²+12=0
5. приведем подобные и получим:
-3х²-х+14=0
для удобства умножим все на -1 ( не обязательно):
3х²+х-14=0
6.D= в²-4ас
D= 1+168=169=13²
х1=-1+13\6=2
х2= -1-13\6= -7\3
ответ: -7\3, 2