ответ: рисунок В .
Уравнение прямой имеет вид y = kx + b .
Чтобы определить, на каком рисунке начерчена прямая y = -2x - 2 , надо обратить внимание на коэффициент перед переменной х .
k= -2 < 0
Так как k<0 , то прямая будет наклонена к положительному направлению оси ОХ под тупым углом . Это видно на рисунке Б и В .
Значит рисунки А и Г не рассматриваем .
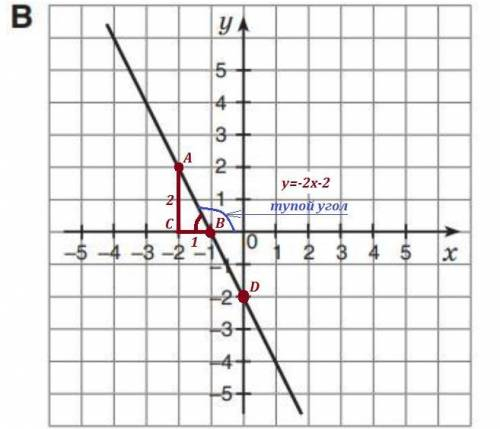
Чтобы убедиться, что k= -2 , строим прямоугольный ΔАВС , ∠С=90° .
Точка В - точка пересечения прямой и оси ОХ , точка А - узловая точка на прямой . Находим отношение АС/ВС=2/1=2 . Значит, действительно коэффициент равен 2 с минусом , то есть k= -2 .
( Минус добавляем из-за того, что угол наклона тупой . )
Теперь определим свободный член . По условию он равен b= -2 . Значит ордината точки пересечения прямой с осью ОУ должна быть равна -2 .
На чертеже точкa пересечения прямой с осью ОУ - это точка
D( 0 ; -2 ) имеет ординату, равную -2 . ( Кстати, на чертеже Б
ордината точки пересечения прямой с осью ОУ равна 2, поэтому
этот рисунок не годится . )
Замечание . На рис. А - прямая у= 2х-2 , на рис. Б - прямая у= -2х+2 ,
на рис. Г - прямая у=2х+2 .
Основні властивості прямокутника:
Діагоналі прямокутника рівні.
Діагоналі прямокутника перетинаються і точкою перетину діляться навпіл.
Діагоналі прямокутника ділять його на два рівні трикутники.
Висоти прямокутника є одночасно і його сторонами.
Навколо будь-якого прямокутника можна описати коло, причому діагональ прямокутника дорівнює діаметру даного кола.
Квадрат діагоналі прямокутника дорівнює сумі квадратів двох його не протилежних сторін.
Прямокутник є плоскою геометричною фігурою, його аналогом у тривимірному просторі є прямокутний паралелепіпед.
Властивості ромба:
Кожен ромб має дві діагоналі, що з'єднують пари протилежних вершин, і має дві пари паралельних сторін. Використовуючи правила конгруентних трикутників, можна довести, що ромб є симетричним відносно кожної з його діагоналей. Звідси випливає, що ромб має такі властивості:
Це паралелограм, діагоналі якого розділяють внутрішній кут.
Протилежні кути ромба рівні.
Діагоналі ромба перетинаються під прямим кутом, точка перетину є серединою кожної діагоналі.
Діагоналі ромба є бісектрисами кутів, з яких вони проведені.
Сторони ромба попарно паралельні.
Точка перетину діагоналей називається центром симетрії ромба.
В будь-який ромб можна вписати коло.
Центром кола, вписаного в ромб, є точка перетину його діагоналей.
Сума квадратів діагоналей дорівнює квадрату сторони, помноженому на чотири: AC2 + BD2 = 4AB2
Однією з основних властивостей є те, що ромб - це паралелограм, внаслідок чого ромб має усі ті властивості, що й паралелограм. Наприклад,
протилежні сторони паралельні;
прилеглі кути є суміжними;
дві діагоналі поділяють одна одну навпіл;
будь-яка пряма, що проходить через центр, поділяє площу навпіл;
сума квадратів сторін дорівнює сумі квадратів діагоналей (правило паралелограма).
Отож, якщо позначити сторону як a, а діагоналі як d1 і d2, то для кожного ромба
Не кожен паралелограм є ромбом, але кожен паралелограм, у якого діагоналі є перпендикулярними, є ромбом. В загальному випадку будь-який чотирикутник з перпендикулярними діагоналями, одна з яких є лінією симетрії, - це дельтоїд.
Властивості квадрата:
У квадрат завжди можна вписати коло;
Навколо квадрата завжди можна описати коло.
Як і в будь-якого опуклого чотирикутника, в квадрата:
Сума всіх внутрішніх кутів дорівнює 2π (360°).
Як і в будь-якому прямокутнику:
Протилежні сторони паралельні.
Діагоналі діляться точкою перетину навпіл.
Точка перетину діагоналей є центром симетрії квадрата.
Діагоналі рівні між собою.
Як і в будь-якому ромбі:
Діагоналі є бісектрисами кутів.
Діагоналі перетинаються під прямим кутом.
Діагоналі є осями симетрії.
Объяснение: